【答案】
分析:(Ⅰ)把m=2代入函数g(x)中,进而求得g(x)的函数表达式,进而根据二次函数的性质求得g(x)的单调区间.
(Ⅱ)由题意可知|x-m|=|m|在x∈[-4,+∞)恒有唯一解.进而分别看x-m=-m和x-m=m时根据x的范围求得m的 范围.
(Ⅲ)通过分析题设条件可知f(x)的值域应是g(x)的值域的子集.进而看当4≤m≤8,m>8,0<m<4和m≤0根据g(x)的单调性求得m的范围.
解答:解:(Ⅰ)m=2时,
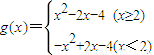
,
函数g(x)的单调增区间为(-∞,1),(2,+∞),单调减区间为(1,2).
(Ⅱ)由f(x)=2
|x-m|在x∈[-4,+∞)恒有唯一解,2
|x-m|=2
|m|,得|x-m|=|m|在x∈[-4,+∞)
恒有唯一解.当x-m=-m时,得x=0∈[-4,+∞);
当x-m=m时,得x=2m,则2m=0或2m<-4,即m<-2或m=0.
综上,m的取值范围是m<-2或m=0.
(Ⅲ)
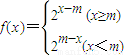
,则f(x)的值域应是g(x)的值域的子集.
①当4≤m≤8时,f(x)在(-∞,4]上单调减,
故f(x)≥f(4)=2
m-4,g(x)在[4,m]上单调减,[m,+∞)上单调增,
故g(x)≥g(m)=2m-8,
所以2
m-4≥2m-8,解得4≤m≤5或m≥6.
②当m>8时,f(x)在(-∞,4]上单调减,
故f(x)≥f(4)=2
m-4,g(x)在

单调增,
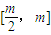
上单调减,[m,+∞)上单调增,g(4)=4m-16>g(m)=2m-8
故g(x)≥g(m)=2m-8,所以2
m-4≥2m-8,解得4≤m≤5或m≥6.
③0<m<4时,f(x)在(-∞,m]上单调减,[m,4]上单调增,故f(x)≥f(m)=1.g(x)在[4,+∞)上单调增,故g(x)≥g(4)=8-2m,
所以8-2m≤1,即
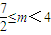
.
④m≤0时,f(x)在(-∞,m]上单调减,[m,4]上单调增,故f(x)≥f(m)=1.g(x)在[4,+∞)上单调增,
故g(x)≥g(4)=8-2m,所以8-2m≤1,即
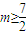
.(舍去)
综上,m的取值范围是

.
点评:本题主要考查了函数单调性和及单调区间的问题.函数单调性的问题是函数的基础知识,应熟练掌握.

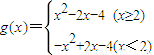 ,
,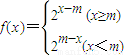 ,则f(x)的值域应是g(x)的值域的子集.
,则f(x)的值域应是g(x)的值域的子集. 单调增,
单调增,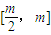 上单调减,[m,+∞)上单调增,g(4)=4m-16>g(m)=2m-8
上单调减,[m,+∞)上单调增,g(4)=4m-16>g(m)=2m-8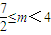 .
.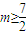 .(舍去)
.(舍去) .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案