
已知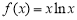 .
.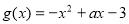 .
.
(1)求函数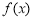 在区间
在区间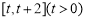 上的最小值;
上的最小值;
(2)对一切实数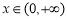 ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3) 证明对一切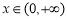 ,
, 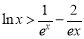 恒成立.
恒成立.
(1)见解析;(2)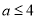 ;(3)见解析.
;(3)见解析.
【解析】
试题分析:(1)对于研究非常规的初等函数的最值问题,往往都需要求函数的导数.根据函数导数的正负判断函数的单调性,利用单调性求函数在某个区间上的最值;(2)恒成立问题,一般都需要将常数和变量分离开来(分离常数法)转化为最值问题处理;(3)证明不等式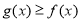 恒成立问题,往往将不等式转化为函数
恒成立问题,往往将不等式转化为函数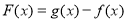 来证明
来证明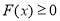 恒成立问题.但有些时候这样转化后不等会乃然很难实现证明,还需对不等式经行恒等变形以达到化简不等式的目的,然后再证.
恒成立问题.但有些时候这样转化后不等会乃然很难实现证明,还需对不等式经行恒等变形以达到化简不等式的目的,然后再证.
试题解析:⑴ 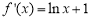 ,当
,当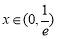 ,
,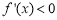 ,
,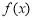 单调递减,
单调递减,
当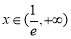 ,
,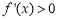 ,
,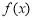 单调递增. 1分
单调递增. 1分
(由于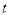 的取值范围不同导致
的取值范围不同导致 所处的区间函数单调性不同,故对
所处的区间函数单调性不同,故对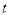 经行分类讨论.)
经行分类讨论.)
① 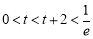 ,t无解; 2分
,t无解; 2分
②  ,即
,即 时,
时,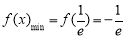 3分
3分
③ 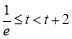 ,即
,即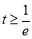 时,
时,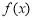 在
在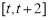 上单调递增,
上单调递增,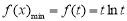 ;
;
所以 5分
5分
由题可知: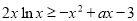 ,则
,则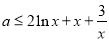 .因对于
.因对于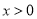 ,
,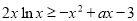 恒成立,故
恒成立,故 ,
,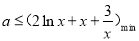
设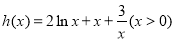 ,则
,则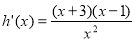 .
.
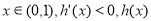 单调递增,
单调递增,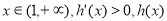 单调递减.
单调递减.
所以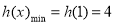 ,即
,即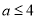 .
.
问题等价于证明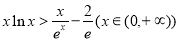 (为了利用第(1)小问结论,并考虑到作差做函数证明不方便,下证
(为了利用第(1)小问结论,并考虑到作差做函数证明不方便,下证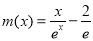 的最值与
的最值与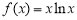 最值的关系.)
最值的关系.)
由(1)可知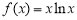 在
在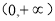 的最小值是
的最小值是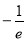 ,当且仅当
,当且仅当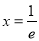 时取到.
时取到.
设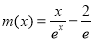 ,则
,则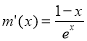 ,易得
,易得 ,当且仅当
,当且仅当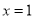 时取到.
时取到.
从而对于一切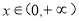 ,都有
,都有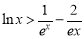 恒成立.
恒成立.
考点:(1)含参量函数最值的讨论;(2)含参恒成立问题,参数取值范围;(3)利用倒数证明不等式.


科目:高中数学 来源:2015届辽宁省抚顺市六校高二下学期期末考试理科数学试卷(解析版) 题型:解答题
为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| 关注NBA | 不关注NBA | 合 计 |
男 生 |
| 6 |
|
女 生 | 10 |
|
|
合 计 |
|
| 48 |
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为2/3
⑴请将上面列连表补充完整,并判断是否有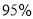 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?
⑵现从女生中抽取2人进一步调查,设其中关注NBA的女生人数为X,求X的分布列与数学期望.
附: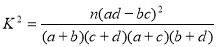 ,其中
,其中 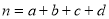
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二新疆班下学期期末数学试卷(解析版) 题型:选择题
口袋中有n(n∈N*)个白球,3个红球.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为X.若P(X=2)=,则n的值为( )
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二新疆班下学期期末数学试卷(解析版) 题型:选择题
用数学归纳法证明1+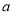 +
+ +…+
+…+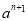 =-
=-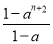 (
(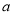 ≠1,n∈N*),在验证n=1成立时,左边的项是( )
≠1,n∈N*),在验证n=1成立时,左边的项是( )
A.1 B.1+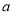 C.1+
C.1+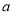 +
+ D.1+
D.1+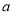 +
+ +
+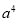
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二下学期期末考试理科数学试卷(解析版) 题型:选择题
函数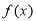 的定义域为开区间
的定义域为开区间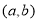 ,其导函数
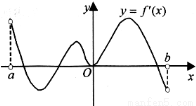
,其导函数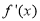 在
在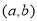 内的图象如图所示,则函数
内的图象如图所示,则函数 在开区间
在开区间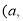
 内极小值点的个数为( )
内极小值点的个数为( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市五校高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知圆G: 经过椭圆
经过椭圆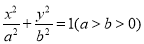 的右焦点F及上顶点B,过椭圆外一点(m,0)(
的右焦点F及上顶点B,过椭圆外一点(m,0)( )倾斜角为
)倾斜角为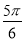 的直线L交椭圆与C、D两点.
的直线L交椭圆与C、D两点.
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的内部,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com