
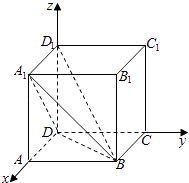
【题目】长方体ABCD﹣A1B1C1D1中,AB=2,AA1=1,若二面角A1﹣BD﹣A的大小为 ![]() ,则BD1与面A1BD所成角的正弦值为 .
,则BD1与面A1BD所成角的正弦值为 .
【答案】![]()
【解析】解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设AD=t,则D(0,0,0),A1(t,0,1),B(t,2,0),D1(0,0,1),![]() =(t,0,1),
=(t,0,1), ![]() =(t,2,0),
=(t,2,0),
设平面DA1B的法向量 ![]() =(x,y,z),
=(x,y,z),
则 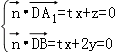 ,取x=2,得
,取x=2,得 ![]() =(2,﹣t,﹣2t),
=(2,﹣t,﹣2t),
又平面ABD的法向量 ![]() =(0,0,1),二面角A1﹣BD﹣A的大小为
=(0,0,1),二面角A1﹣BD﹣A的大小为 ![]() ,
,
∴|cos< ![]() >|=
>|= ![]() =
= ![]() =cos
=cos ![]() ,解得t=2
,解得t=2 ![]() ,或t=﹣2
,或t=﹣2 ![]() (舍),
(舍),
∴B(2 ![]() ,2,0),
,2,0), ![]() =(﹣2
=(﹣2 ![]() ,﹣2,1),
,﹣2,1), ![]() =(2,﹣2
=(2,﹣2 ![]() ,﹣4
,﹣4 ![]() ),
),
设BD1与面A1BD所成角为θ,
sinθ= 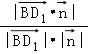 =
= ![]() =
= ![]() .
.
∴BD1与面A1BD所成角的正弦值为 ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用异面直线及其所成的角对题目进行判断即可得到答案,需要熟知异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.


科目:高中数学 来源: 题型:
【题目】(2015·新课标1卷)已知椭圆E的中心为坐标原点,离心率为![]() , E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|= ( )
, E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|= ( )
A.3
B.6
C.9
D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点. 
(1)证明:DQ∥平面CPM;
(2)若二面角C﹣AB﹣D的大小为 ![]() ,求∠BDC的正切值.
,求∠BDC的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f( ![]() )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f( ![]() )>f(π),则f(x)的单调递增区间是( )
)>f(π),则f(x)的单调递增区间是( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ,kπ+ ![]() ](k∈Z)
](k∈Z)
C.[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
D.[kπ﹣ ![]() ,kπ](k∈Z)
,kπ](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣1.
(1)对于任意的1≤x≤2,不等式4m2|f(x)|+4f(m)≤|f(x﹣1)|恒成立,求实数m的取值范围;
(2)若对任意实数x1∈[1,2].存在实数x2∈[1,2],使得f(x1)=|2f(x2)﹣ax2|成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+2bx+c,设函数g(x)=|f(x)|在区间[﹣1,1]上的最大值为M.
(1)若b=2,试求出M;
(2)若M≥k对任意的b、c恒成立,试求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以“赏中华诗词,寻文化基因,品生活之美”为宗旨的《中国诗词大会》,是央视科教频道推出的一档大型演播室文化益智节目,每季赛事共分为10场,每场分个人追逐赛与擂主争霸赛两部分,其中擂主争霸赛在本场个人追逐赛的优胜者与上一场擂主之间进行,一共备有9道抢答题,选手抢到并答对获得1分,答错对方得1分,当有一个选手累计得分达到5分时比赛结束,该选手就是本场的擂主,在某场比赛中,甲、乙两人进行擂主争霸赛,设每个题目甲答对的概率都为 ![]() ,乙答对的概率为
,乙答对的概率为 ![]() ,每道题目都有人抢答,且每人抢到答题权的概率均为
,每道题目都有人抢答,且每人抢到答题权的概率均为 ![]() ,各题答题情况互不影响. (Ⅰ)求抢答一道题目,甲得1分的概率;
,各题答题情况互不影响. (Ⅰ)求抢答一道题目,甲得1分的概率;
(Ⅱ)现在前5题已经抢答完毕,甲得2分,乙得3分,在接下来的比赛中,设甲的得分为ξ,求ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形BCEF所成角的二面角的平面角的大小是 ![]() ,PQ是正方形BDEF所在平面内的一条动直线,则直线BD与PQ所成角的取值范围是( )
,PQ是正方形BDEF所在平面内的一条动直线,则直线BD与PQ所成角的取值范围是( ) 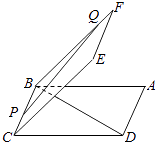
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={a1 , a2 , …,an},ai∈R,i=1,2,…,n,并且n≥2. 定义 ![]() (例如:
(例如: ![]() ).
).
(Ⅰ)若A={1,2,3,4,5,6,7,8,9,10},M={1,2,3,4,5},集合A的子集N满足:N≠M,且T(M)=T(N),求出一个符合条件的N;
(Ⅱ)对于任意给定的常数C以及给定的集合A={a1 , a2 , …,an},求证:存在集合B={b1 , b2 , …,bn},使得T(B)=T(A),且 ![]() .
.
(Ⅲ)已知集合A={a1 , a2 , …,a2m}满足:ai<ai+1 , i=1,2,…,2m﹣1,m≥2,a1=a,a2m=b,其中a,b∈R为给定的常数,求T(A)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com