
【题目】如图,在三棱锥A﹣BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点. 
(1)证明:DQ∥平面CPM;
(2)若二面角C﹣AB﹣D的大小为 ![]() ,求∠BDC的正切值.
,求∠BDC的正切值.
【答案】
(1)证明:取AB的中点E,

则 ![]() ,所以EQ∥PC.
,所以EQ∥PC.
又EQ平面CPM,所以EQ∥平面CPM.
又PM是△BDE的中位线,所以DE∥PM,
从而DE∥平面CPM.
所以平面DEQ∥平面CPM,
故DQ∥平面CPM.
(2)解法1:由AD⊥平面BCD知,AD⊥CM
由BC=CD,BM=MD,知BD⊥CM,
故CM⊥平面ABD.
由(1)知DE∥PM,而DE⊥AB,故PM⊥AB.
所以∠CPM是二面角C﹣AB﹣D的平面角,
即 ![]() .
.
设PM=a,则 ![]() ,
, ![]() ,
,
在Rt△CMD中, ![]() .
.
所以∠BDC的正切值为 ![]() .
.
解法2:以M为坐标原点,MC,MD,ME所在的直线分别为x轴,y轴,z轴,
建立如图所示的空间直角坐标系.
设MC=a,MD=b,则C(a,0,0),B(0,﹣b,0),A(0,b,2b)
则 ![]() ,
, ![]()
设 ![]() 平面ABC的一个法向量,
平面ABC的一个法向量,
则  即
即 ![]() 取
取 ![]()
平面ABD的一个法向量为 ![]() ,
,
所以 ![]() ,所以
,所以 ![]()
在Rt△CMD中, ![]()
所以∠BDC的正切值为 ![]() .
.
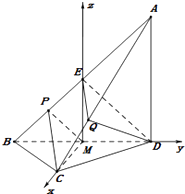
【解析】(1)取AB的中点E,则EQ∥PC,从而EQ∥平面CPM,由中位线定理得DE∥PM,从而DE∥平面CPM,进而平面DEQ∥平面CPM,由此能证明DQ∥平面CPM.(2)法1:推导出AD⊥CM,BD⊥CM,从而CM⊥平面ABD,进而得到∠CPM是二面角C﹣AB﹣D的平面角,由此能求出∠BDC的正切值.法2:以M为坐标原点,MC,MD,ME所在的直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出∠BDC的正切值.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣1|+|x﹣2|
(1)求不等式f(x)≤3的解集;
(2)若不等式||a+b|﹣|a﹣b||≤|a|f(x)(a≠0,a∈R,b∈R)恒成立,求实数x的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(﹣1,4)及圆C:(x﹣2)2+(y﹣3)2=1.则下列判断正确的序号为 .
①点P在圆C内部;
②过点P做直线l,若l将圆C平分,则l的方程为x+3y﹣11=0;
③过点P做直线l与圆C相切,则l的方程为y﹣4=0或3x+4y﹣13=0;
④一束光线从点P出发,经x轴反射到圆C上的最短路程为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PC⊥平面ABCD,AB∥DC,DC⊥AC.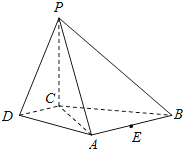
(1)求证:DC⊥平面PAC;
(2)求证:平面PAB⊥平面PAC;
(3)设点E为AB的中点,在棱PB上是否存在点F,使得PA∥平面CEF?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,内角A,B,C所对的边分别是a,b,c,已知sinAsinB=sinCtanC.
(1)求 ![]() 的值:
的值:
(2)若a= ![]() c,且△ABC的面积为4,求c的值.
c,且△ABC的面积为4,求c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com