
已知函数 ,其中m,a均为实数.
,其中m,a均为实数.
(1)求 的极值;
的极值;
(2)设 ,若对任意的
,若对任意的
 ,
, 恒成立,求
恒成立,求 的最小值;
的最小值;
(3)设 ,若对任意给定的
,若对任意给定的 ,在区间
,在区间 上总存在
上总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
(1)极大值为1,无极小值;(2)3?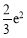 ;(3)
;(3)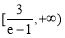 .
.
【解析】
试题分析:(1)求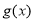 的极值,就是先求出
的极值,就是先求出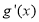 ,解方程
,解方程 ,此方程的解把函数的定义域分成若干个区间,我们再确定在每个区间里
,此方程的解把函数的定义域分成若干个区间,我们再确定在每个区间里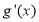 的符号,从而得出极大值或极小值;(2)此总是首先是对不等式
的符号,从而得出极大值或极小值;(2)此总是首先是对不等式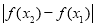

 恒成立的转化,由(1)可确定
恒成立的转化,由(1)可确定 在
在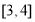 上是增函数,同样的方法(导数法)可确定函数
上是增函数,同样的方法(导数法)可确定函数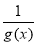 在
在 上也是增函数,不妨设
上也是增函数,不妨设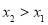 ,这样题设绝对值不等式可变为
,这样题设绝对值不等式可变为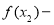



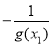 ,整理为
,整理为 ,由此函数
,由此函数 在区间
在区间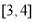 上为减函数,则
上为减函数,则 在(3,4)上恒成立,要求
在(3,4)上恒成立,要求 的取值范围.采取分离参数法得
的取值范围.采取分离参数法得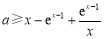 恒成立,于是问题转化为求
恒成立,于是问题转化为求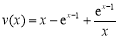 在
在 上的最大值;(3)由于
上的最大值;(3)由于 的任意性,我们可先求出
的任意性,我们可先求出 在
在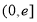 上的值域
上的值域 ,题设“在区间
,题设“在区间 上总存在
上总存在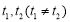 ,使得
,使得

 成立”,转化为函数
成立”,转化为函数 在区间
在区间 上不是单调函数,极值点为
上不是单调函数,极值点为 (
( ),其次
),其次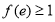 ,极小值
,极小值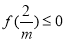 ,最后还要证明在
,最后还要证明在 上,存在
上,存在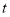 ,使
,使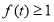 ,由此可求出
,由此可求出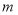 的范围.
的范围.
试题解析:(1)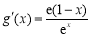 ,令
,令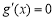 ,得x=1. 1分
,得x=1. 1分
列表如下:
x | (?∞,1) | 1 | (1,∞) |
| | 0 | ? |
g(x) | ↗ | 极大值 | ↘ |
∵g(1)=1,∴y= 的极大值为1,无极小值. 3分
的极大值为1,无极小值. 3分
(2)当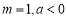 时,
时, ,
,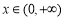 .
.
∵ 在
在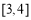 恒成立,∴
恒成立,∴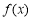 在
在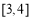 上为增函数. 4分
上为增函数. 4分
设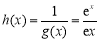 ,∵
,∵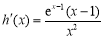 >0在
>0在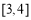 恒成立,
恒成立,
∴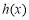 在
在 上为增函数. 5分
上为增函数. 5分
设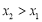 ,则
,则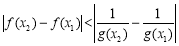 等价于
等价于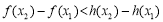 ,
,
即 .
.
设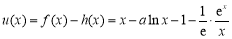 ,则u(x)在
,则u(x)在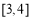 为减函数.
为减函数.
∴ 在(3,4)上恒成立. 6分
在(3,4)上恒成立. 6分
∴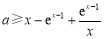 恒成立.
恒成立.
设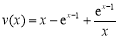 ,∵
,∵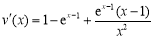 =
=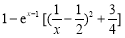 ,x?[3,4],
,x?[3,4],
∴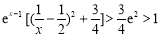 ,∴
,∴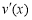 <0,
<0,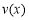 为减函数.
为减函数.
∴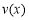 在[3,4]上的最大值为v(3)=3?
在[3,4]上的最大值为v(3)=3?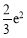 . 8分
. 8分
∴a≥3?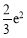 ,∴
,∴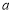 的最小值为3?
的最小值为3?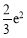 . 9分
. 9分
(3)由(1)知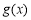 在
在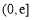 上的值域为
上的值域为 . 10分
. 10分
∵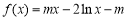 ,
,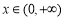 ,
,
当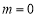 时,
时, 在
在 为减函数,不合题意. 11分
为减函数,不合题意. 11分
当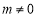 时,
时, ,由题意知
,由题意知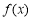 在
在 不单调,
不单调,
所以 ,即
,即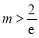 .① 12分
.① 12分
此时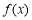 在
在 上递减,在
上递减,在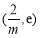 上递增,
上递增,
∴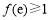 ,即
,即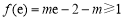 ,解得
,解得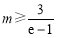 .②
.②
由①②,得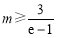 . 13分
. 13分
∵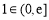 ,∴
,∴ 成立. 14分
成立. 14分
下证存在 ,使得
,使得 ≥1.
≥1.
取 ,先证
,先证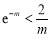 ,即证
,即证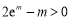 .③
.③
设 ,则
,则 在
在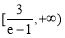 时恒成立.
时恒成立.
∴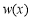 在
在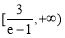 时为增函数.∴
时为增函数.∴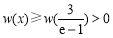 ,∴③成立.
,∴③成立.
再证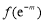 ≥1.
≥1.
∵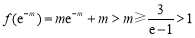 ,∴
,∴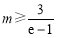 时,命题成立.
时,命题成立.
综上所述,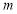 的取值范围为
的取值范围为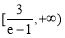 . 16分
. 16分
考点:导数的应用,求单调区间,极值,求函数的值域,不等式恒成立等函数的综合应用.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数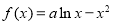 .
.
(1)当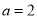 时,求函数
时,求函数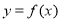 在
在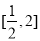 上的最大值;
上的最大值;
(2)令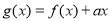 ,若
,若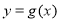 在区间
在区间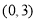 上不单调,求
上不单调,求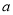 的取值范围;
的取值范围;
(3)当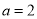 时,函数
时,函数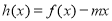 的图像与x轴交于两点
的图像与x轴交于两点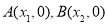 ,且
,且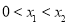 ,又
,又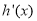 是
是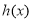 的导函数,若正常数
的导函数,若正常数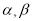 满足条件
满足条件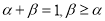 .证明:
.证明: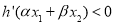 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
公比为2的等比数列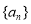 的各项都是正数,且
的各项都是正数,且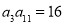 则
则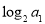 = ( )
= ( )
A.4 B.-4 C.2 D.-2
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省连云港市高三3月第二次调研考试理科数学试卷(解析版) 题型:解答题
甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为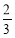 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数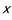 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省连云港市高三3月第二次调研考试理科数学试卷(解析版) 题型:解答题
设函数 .
.
(1)求 的最小正周期和值域;
的最小正周期和值域;
(2)在锐角△ 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 且
且 ,
, ,求
,求 和
和 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省连云港市高三3月第二次调研考试理科数学试卷(解析版) 题型:填空题
从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com