
已知函数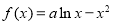 .
.
(1)当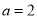 时,求函数
时,求函数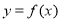 在
在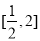 上的最大值;
上的最大值;
(2)令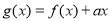 ,若
,若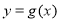 在区间
在区间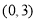 上不单调,求
上不单调,求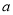 的取值范围;
的取值范围;
(3)当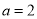 时,函数
时,函数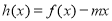 的图像与x轴交于两点
的图像与x轴交于两点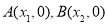 ,且
,且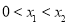 ,又
,又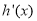 是
是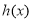 的导函数,若正常数
的导函数,若正常数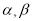 满足条件
满足条件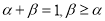 .证明:
.证明: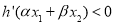 .
.
(1)-1;(2)  ;(3)参考解析
;(3)参考解析
【解析】
试题分析:(1)因为函数 ,当
,当 时.求出函数
时.求出函数 的导数,即可得到
的导数,即可得到 上函数的单调性,从而得到函数的最大值.
上函数的单调性,从而得到函数的最大值.
(2)因为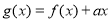 ,若
,若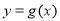 在区间
在区间 上不单调,即等价于函数
上不单调,即等价于函数 在(0,3)上有实数解,且无重根.所以由
在(0,3)上有实数解,且无重根.所以由 ,分离变量
,分离变量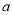 ,通过研究函数
,通过研究函数 ,
, 的范围,即可得到
的范围,即可得到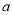 取值范围.
取值范围.
(3)因为当 时,函数
时,函数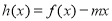 的图像与x轴交于两点
的图像与x轴交于两点 ,所以可得
,所以可得 即可用
即可用 表示m.又由
表示m.又由 化简.可消去m.即可得到
化简.可消去m.即可得到 关于
关于 的代数式,再利用导数知识求出
的代数式,再利用导数知识求出 的最值即可得结论.
的最值即可得结论.
试题解析:(1) 
函数 在[
在[ ,1]是增函数,在[1,2]是减函数,
,1]是增函数,在[1,2]是减函数,
所以 .
.
(2)因为 ,所以
,所以 ,
,
因为 在区间
在区间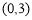 上不单调,所以
上不单调,所以 在(0,3)上有实数解,且无重根,
在(0,3)上有实数解,且无重根,
由 ,有
,有 =
= ,(
,( )
)
所以

(3)∵ ,又
,又 有两个实根
有两个实根 ,
,
∴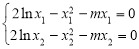 ,两式相减,得
,两式相减,得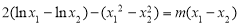 ,
,
∴ ,
,
于是
 .
.
 .
.
要证: ,只需证:
,只需证:
只需证: .(*)
.(*)
令 ,∴(*)化为
,∴(*)化为 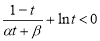 ,只证
,只证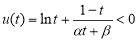 即可.
即可. 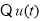 在(0,1)上单调递增,
在(0,1)上单调递增, ,即
,即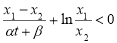 .
.
∴ .
.
考点:1.函数的最值.2.函数的单调性的应用.3.等价变换数学思想.4.换元的数学思想.5.运算量较大属于有难度题型.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
方程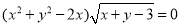 表示的曲线是( )
表示的曲线是( )
A.一个圆和一条直线 B.一个圆和一条射线 C.一个圆 D.一条直线
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省高三联合考试理科数学试卷(解析版) 题型:选择题
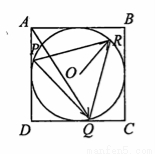
如图,四边形ABCD是半径为1的圆O的外切正方形,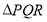 是圆O的内接正三角形,当
是圆O的内接正三角形,当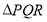 绕着圆心O旋转时,
绕着圆心O旋转时,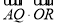 的取值范围是( )
的取值范围是( )
A.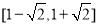 B.
B.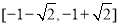
C.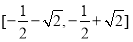 D.
D.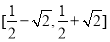
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省高三联合考试文科数学试卷(解析版) 题型:选择题
记集合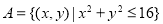 和集合
和集合 表示的平面区域分别为
表示的平面区域分别为 若在区域
若在区域 内任取一点
内任取一点 ,则点M落在区域
,则点M落在区域 的概率为( )
的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
设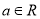 函数
函数 满足
满足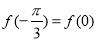 .
.
(1)求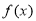 的单调递减区间;
的单调递减区间;
(2)设锐角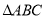 的内角
的内角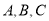 所对的边分别为
所对的边分别为 ,且
,且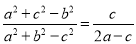 ,求
,求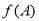 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
菱形ABCD的边长为 ,
,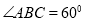 ,沿对角线AC折成如图所示的四面体,二面角B-AC-D为
,沿对角线AC折成如图所示的四面体,二面角B-AC-D为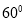 ,M为AC的中点,P在线段DM上,记DP=x,PA+PB=y,则函数y=f(x)的图象大致为( )
,M为AC的中点,P在线段DM上,记DP=x,PA+PB=y,则函数y=f(x)的图象大致为( )


查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试文科数学试卷(解析版) 题型:填空题
如图所示将若干个点摆成三角形,每条边(包括两个端点)有 个点,相应的图案中总的点数记为
个点,相应的图案中总的点数记为 ,则
,则 _______.
_______.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省连云港市高三3月第二次调研考试理科数学试卷(解析版) 题型:解答题
已知函数 ,其中m,a均为实数.
,其中m,a均为实数.
(1)求 的极值;
的极值;
(2)设 ,若对任意的
,若对任意的
 ,
, 恒成立,求
恒成立,求 的最小值;
的最小值;
(3)设 ,若对任意给定的
,若对任意给定的 ,在区间
,在区间 上总存在
上总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com