
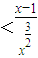 .
.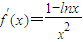 ,当x∈(0,e)时,f′(x)>0;当x∈(e,+∞)时,f′(x)<0,故f(x)在(0,e]上递增,在[e,+∞)递减.
,当x∈(0,e)时,f′(x)>0;当x∈(e,+∞)时,f′(x)<0,故f(x)在(0,e]上递增,在[e,+∞)递减. =
=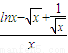 ,记
,记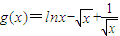 ,
,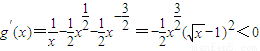 ,g(x)在(1,+∞)为减函数,由此能够证明f(x)
,g(x)在(1,+∞)为减函数,由此能够证明f(x)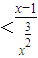 .
.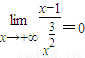 ,且
,且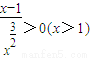 ,
,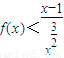 ,当x→∞时,f(x)→0,由此能求出求出a的取值范围.
,当x→∞时,f(x)→0,由此能求出求出a的取值范围.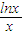 ,
,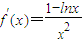 ,
,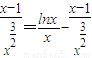 =
=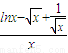 ,
,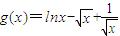 ,
,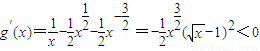 ,
,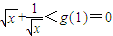 ,
,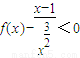 ,即f(x)
,即f(x)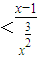 .
. ,且
,且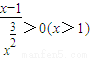 ,
,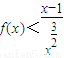 ,
,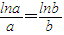 ,∴ab=ba,此时1<a<e.
,∴ab=ba,此时1<a<e.

科目:高中数学 来源: 题型:
| p | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知y=Asin(ωx+?)的最大值为1,在区间[
已知y=Asin(ωx+?)的最大值为1,在区间[| π |
| 6 |
| 2π |
| 3 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、以上都不是 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1-x | 3 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省兰州一中高三(上)12月月考数学试卷(文科)(解析版) 题型:选择题
 上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )
上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )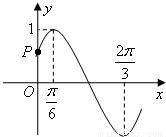



查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省龙岩市高三(上)期末质量检查一级达标数学试卷(文科)(解析版) 题型:解答题
 -2lnx、
-2lnx、查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com