
(本小题满分15分)已知函数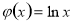
(Ⅰ)若曲线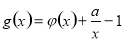 在点
在点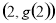 处的切线与直线
处的切线与直线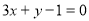 平行,求
平行,求 的值;
的值;
(Ⅱ)记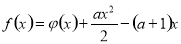 ,
,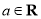 ,且
,且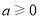 .求函数
.求函数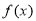 的单调递增区间.
的单调递增区间.
(Ⅰ)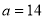 ;(Ⅱ)当
;(Ⅱ)当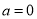 时,函数
时,函数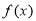 的递增区间是
的递增区间是 ;当
;当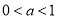 时,函数
时,函数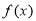 的递增区间是
的递增区间是 ,
,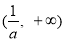 ;当
;当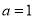 时,函数
时,函数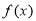 的递增区间是
的递增区间是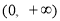 ;当
;当 时,函数
时,函数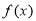 的递增区间是
的递增区间是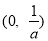 ,
,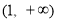 .
.
【解析】
试题分析:(Ⅰ)先求导,由导数的几何意义可得在点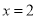 的导数即为在此点处切线的斜率。从而可得
的导数即为在此点处切线的斜率。从而可得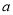 的值。(Ⅱ)先求导整理可得
的值。(Ⅱ)先求导整理可得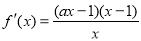 ,当
,当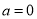 时,
时,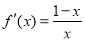 ,解导数大于0可得增区间;当
,解导数大于0可得增区间;当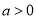 时,导数等于0的两根为
时,导数等于0的两根为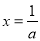 或
或 ,注意对两根大小的讨论,同样解导数大于0可得增区间。
,注意对两根大小的讨论,同样解导数大于0可得增区间。
试题解析:(Ⅰ)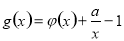 =
=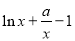 (
(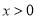 ),
), (
(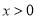 ),
),
因为曲线 在点
在点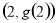 处的切线与直线
处的切线与直线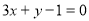 平行,
平行,
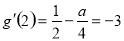 ,解得
,解得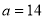 .
.
(Ⅱ)因为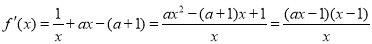
(1)当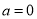 时,
时,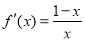 .令
.令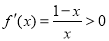 解得
解得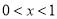
(2)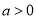 时
时
令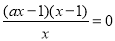 ,解得
,解得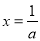 或
或 .
.
(ⅰ)当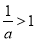 即
即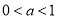 时,
时,
由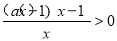 ,及
,及 得
得  .
.
解得 ,或
,或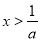 ;
;
(ⅱ)当 即
即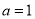 时,
时,
因为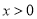 ,
,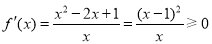 恒成立.
恒成立.
(ⅲ)当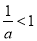 即
即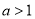 时,由
时,由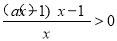 ,及
,及 得
得 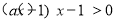 .
.
解得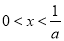 ,或
,或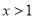 .
.
综上所述,
当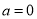 时,函数
时,函数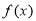 的递增区间是
的递增区间是 ;
;
当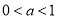 时,函数
时,函数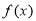 的递增区间是
的递增区间是 ,
,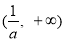 ;
;
当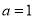 时,函数
时,函数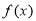 的递增区间是
的递增区间是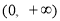 ;
;
当 时,函数
时,函数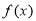 的递增区间是
的递增区间是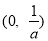 ,
,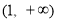 .
.
考点:1导数的几何意义;2用导数研究函数的单调性。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:选择题
从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
A.“至少有一个黑球”与“都是黑球”
B.“至少有一个黑球”与“都是红球”
C.“至少有一个黑球”与“至少有一个红球”
D.“恰有一个黑球”与“恰有两个黑球”
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)文科数学试卷(解析版) 题型:选择题
一个口袋中装有形状和大小完全相同的3个红球和2个白球,甲从这个口袋中任意摸取2个球, 则甲摸得的2个球恰好都是红球的概率是( )
A.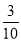 B.
B.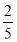 C.
C.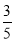 D.
D. 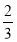
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)理科数学试卷(解析版) 题型:选择题
一个正三棱柱的三视图如图所示,这个三棱柱的侧(左)视图的面积为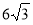 ,则这个三棱柱的体积为 ( )
,则这个三棱柱的体积为 ( )
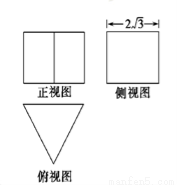
A.12 B.16 C.8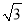 D.12
D.12
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)文科数学试卷(解析版) 题型:填空题
已知定义在R上的函数f(x),g(x)满足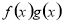 =ax,且f′(x)g(x)+ f(x)·g′(x) <0,
=ax,且f′(x)g(x)+ f(x)·g′(x) <0,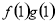 +
+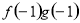 =
=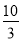 ,若有穷数列{
,若有穷数列{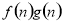 }(n∈N*)的前n项和等于
}(n∈N*)的前n项和等于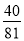 ,则n等于 .
,则n等于 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)文科数学试卷(解析版) 题型:选择题
如图所示,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,则它的涂漆面数为2的概率( )
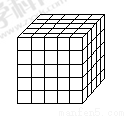
A. B. C. D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省长葛市毕业班第三次质量预测(三模)理科数学试卷(解析版) 题型:解答题
已知函数 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是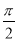 ,且满足,
,且满足,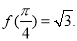
(1)求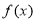 的单调递减区间;
的单调递减区间;
(2)在钝角△ABC中,a、b、c分别为角A、B、C的对边,sinB=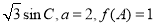 ,求△ABC的面积。
,求△ABC的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com