
已知函数 满足对任意实数
满足对任意实数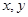 都有
都有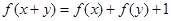 成立,且当
成立,且当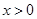 时,
时,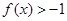 ,
,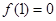 .
.
(1)求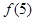 的值;
的值;
(2)判断 在
在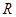 上的单调性,并证明;
上的单调性,并证明;
(3)若对于任意给定的正实数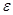 ,总能找到一个正实数
,总能找到一个正实数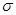 ,使得当
,使得当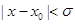 时,
时,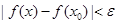 ,则称函数
,则称函数 在
在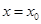 处连续。试证明:
处连续。试证明: 在
在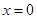 处连续.
处连续.
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
某分公司经销某种品牌产品,每件产品的成本为30元,并且每件产品须向总公司缴纳a元(a为常数,2≤a≤5)的管理费,根据多年的统计经验,预计当每件产品的售价为x元时,产品一年的销售量为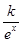 (e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(Ⅰ)求分公司经营该产品一年的利润L(x)万元与每件产品的售价x元的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,该产品一年的利润L(x)最大,并求出L(x)的最大值.
参考公式: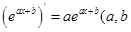 为常数
为常数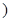 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
统计表明:某种型号的汽车在匀速行驶中每小时的耗油量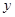 (升)关于行驶速度
(升)关于行驶速度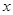 (千米/每小时)的函数解析式可以表示为
(千米/每小时)的函数解析式可以表示为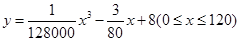 ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大速度行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数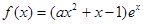 ,其中
,其中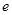 是自然对数的底数,
是自然对数的底数,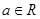 .
.
(1)若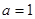 ,求曲线
,求曲线 在点
在点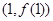 处的切线方程;
处的切线方程;
(2)若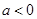 ,求
,求 的单调区间;
的单调区间;
(3)若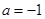 ,函数
,函数 的图象与函数
的图象与函数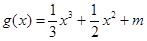 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数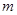 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段,已知跳水板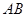 长为2m,跳水板距水面
长为2m,跳水板距水面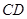 的高
的高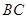 为3m,
为3m, =5m,
=5m,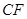 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点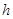 m(
m(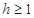 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以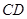 为横轴,
为横轴, 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.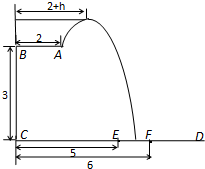
(1)当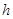 =1时,求跳水曲线所在的抛物线方程;
=1时,求跳水曲线所在的抛物线方程;
(2)若跳水运动员在区域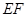 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时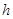 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知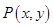 为函数
为函数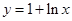 图象上一点,
图象上一点,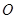 为坐标原点,记直线
为坐标原点,记直线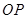 的斜率
的斜率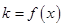 .
.
(1)若函数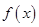 在区间
在区间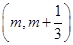
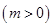 上存在极值,求实数
上存在极值,求实数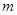 的取值范围;
的取值范围;
(2)当 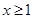 时,不等式
时,不等式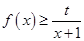 恒成立,求实数
恒成立,求实数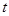 的取值范围;
的取值范围;
(3)求证: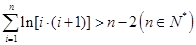 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)已知函数 ,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.
,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.
(I)指出函数f(x)的单调区间;
(II)若函数f(x)的图象在点A,B处的切线互相垂直,且x2<0,求x2﹣x1的最小值;
(III)若函数f(x)的图象在点A,B处的切线重合,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com