
已知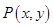 为函数
为函数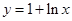 图象上一点,
图象上一点,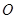 为坐标原点,记直线
为坐标原点,记直线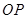 的斜率
的斜率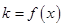 .
.
(1)若函数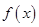 在区间
在区间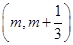
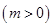 上存在极值,求实数
上存在极值,求实数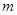 的取值范围;
的取值范围;
(2)当 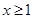 时,不等式
时,不等式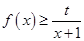 恒成立,求实数
恒成立,求实数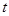 的取值范围;
的取值范围;
(3)求证: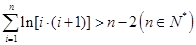 .
.
(1)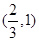 ;(2)
;(2)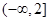 ;(3)证明过程详见解析.
;(3)证明过程详见解析.
解析试题分析:本题主要考查导数的应用、不等式、数列等基础知识,考查思维能力、运算能力和思维的严谨性.第一问,考查求导求极值问题;第二问,是恒成立问题,将第一问的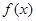 代入,整理表达式,得出
代入,整理表达式,得出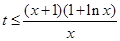 ,构造函数
,构造函数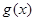 ,下面的主要任务是求出函数
,下面的主要任务是求出函数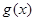 的最小值,所以
的最小值,所以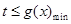 ;第三问,是不等式的证明,先利用放缩法构造出所证不等式的形式,构造数列,利用累加法得到所证不等式的左边,右边利用裂项相消法求和,再次利用放缩法得到结论.
;第三问,是不等式的证明,先利用放缩法构造出所证不等式的形式,构造数列,利用累加法得到所证不等式的左边,右边利用裂项相消法求和,再次利用放缩法得到结论.
试题解析:(1)由题意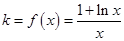 ,
,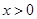 ,所以
,所以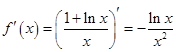 2分
2分
当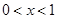 时,
时,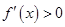 ;当
;当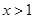 时,
时,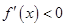 .
.
所以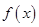 在
在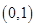 上单调递增,在
上单调递增,在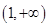 上单调递减,故
上单调递减,故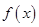 在
在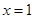 处取得极大值.
处取得极大值.
因为函数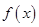 在区间
在区间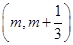 (其中
(其中 )上存在极值,
)上存在极值,
所以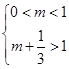 ,得
,得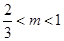 .即实数
.即实数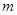 的取值范围是
的取值范围是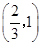 . 4分
. 4分
(2)由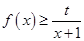 得
得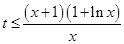 ,令
,令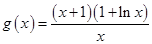 ,
,
则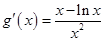 . 6分
. 6分
令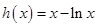 ,则
,则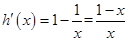 ,
,
因为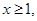 所以
所以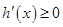 ,故
,故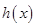 在
在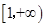 上单调递增. 8分
上单调递增. 8分
所以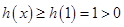 ,从而
,从而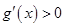
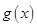 在
在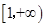 上单调递增,
上单调递增, 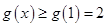
所以实数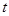 的取值范围是
的取值范围是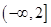 . 10分
. 10分
(3)由(2) 知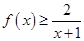 恒成立,
恒成立,
即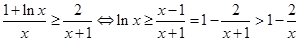 12分
12分
令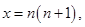 则
则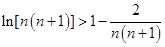 , 14分
, 14分
所以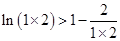 ,
, 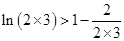 , ,
, ,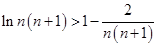 .
.
将以上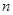 个式子相加得:
个式子相加得: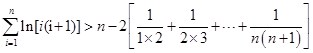
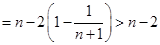 ,
,
故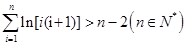 . 16分
. 16分
考点:1.函数极值的求法;2.恒成立问题;3.求函数的最值;4.放缩法;5.裂项相消法.


科目:高中数学 来源: 题型:解答题
已知函数 满足对任意实数
满足对任意实数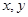 都有
都有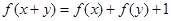 成立,且当
成立,且当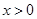 时,
时,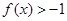 ,
,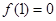 .
.
(1)求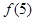 的值;
的值;
(2)判断 在
在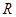 上的单调性,并证明;
上的单调性,并证明;
(3)若对于任意给定的正实数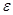 ,总能找到一个正实数
,总能找到一个正实数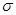 ,使得当
,使得当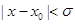 时,
时,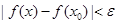 ,则称函数
,则称函数 在
在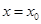 处连续。试证明:
处连续。试证明: 在
在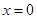 处连续.
处连续.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 的图像与函数h(x)=x++2的图像关于点A(0,1)对称.
的图像与函数h(x)=x++2的图像关于点A(0,1)对称.
(1) 求 的解析式;
的解析式;
(2) 若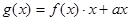 ,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格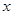 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式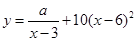 ,其中
,其中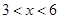 ,
, 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(Ⅰ)求 的值;
的值;
(Ⅱ)若该商品的成本为3元/千克,试确定销售价格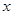 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
渔场中鱼群的最大养殖量是m吨,为保证鱼群的生长空间,实际养殖量不能达到最大养殖量,必须留出适当的空闲量。已知鱼群的年增长量y吨和实际养殖量x吨与空闲率乘积成正比,比例系数为k(k>0).
写出y关于x的函数关系式,指出这个函数的定义域;
求鱼群年增长量的最大值;
当鱼群的年增长量达到最大值时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数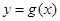 的导函数的图像与直线
的导函数的图像与直线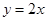 平行,且
平行,且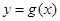 在
在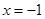 处取得极小值
处取得极小值 .设
.设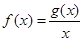 .
.
(1)若曲线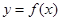 上的点
上的点 到点
到点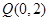 的距离的最小值为
的距离的最小值为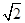 ,求
,求 的值;
的值;
(2) 如何取值时,函数
如何取值时,函数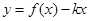 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com