
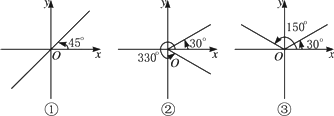
用集合的形式表示与下图中的角的终边相同的角的集合.
|
解:(1)从图①中看出,图中两个角的终边在一条直线上. 在0°-360°范围内,且另一个角为225°,故所求集合为 S={β|β=45°+k·360°,k∈Z}∪{β|β=225°+k·360°,k∈Z} ={β|β=45°+2k·180°,k∈Z}∪{β|β=45°+180°+2k·180°,k∈Z} ={β|β=45°+2k·180°,k∈Z}∪{β|β=45°+(2k+1)·180°,k∈Z} ={β|β=45°+n·180°,n∈Z}. (2)从图②中看出,图中两个角的终边关于x轴对称,故所求集合为 S={β|β=30°+k·360°,k∈Z}∪{β|β=330°+k·360°,k∈Z} ={β|β=30°+k·360°,k∈Z}∪{β|β=-30°+360°+k·360°,k∈Z} ={β|β=30°+k·360°,k∈Z}∪{β|β=-30°+(k+1)·360°,k∈Z} ={β|β=±30°+n·360°,n∈Z}. (3)从图③中看出,图中两个角的终边关于y轴对称,故所求集合为 S={β|β=30°+k·360°,k∈Z}∪{β|β=150°+k·360°,k∈Z} ={β|β=30°+k·360°,k∈Z}∪{β|β=-30°+180°+2k·180°,k∈Z} ={β|β=30°+2k·180°,k∈Z}∪{β|β=-30°+(2k+1)·180°,k∈Z} ={β|β=(-1)n·30°+n·180°,n∈Z}. 思路分析:运用两角关系及终边相同角解决. |
|
本题求解过程中,利用了数形结合的思想.两个集合并为一个集合,应先把两个集合变成一个统一的形式.否则,就不能并为一个集合. |


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
(1)绝对值不大于3的整数组成的集合:__________;
(2)方程(3x-5)(x+2)(x2+3)=0的实数解组成的集合: __________;
(3)一次函数y=x+6图像上所有点组成的集合: __________.
查看答案和解析>>
科目:高中数学 来源:2010年安徽省安庆一中高三第三次模拟考试数学(理)试题 题型:解答题
(本题满分 13分)
集合 为集合
为集合 的
的 个不同的子集,对于任意不大于
个不同的子集,对于任意不大于 的正整数
的正整数 满足下列条件:
满足下列条件:
① ,且每一个
,且每一个 至
至 少含有三个元素;
少含有三个元素;
② 的充要条件是
的充要条件是 (其中
(其中 )。
)。
为了表示这些子集,作 行
行 列的数表(即
列的数表(即 数表),规定第
数表),规定第 行第
行第 列数为:
列数为: 。
。
(1)该表中每一列至少有多少个1;若集合 ,请完成下面
,请完成下面 数表(填符合题意的一种即可);
数表(填符合题意的一种即可);
(2)用含 的代数式表示
的代数式表示 数表
数表 中1的个数
中1的个数 ,并证明
,并证明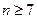 ;
;
(3)设数列 前
前 项和为
项和为 ,数列
,数列 的通项公式为:
的通项公式为: ,证明不等式:
,证明不等式: 对任何正整数
对任何正整数 都成立。
都成立。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com