
【题目】已知函数![]() ,
,![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)若![]() 为单调递增函数,求实数
为单调递增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 存在极小值时,设极小值点为
存在极小值时,设极小值点为![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)若![]() 为单调递增函数,则有
为单调递增函数,则有![]() 恒成立,从而求
恒成立,从而求![]() 的最小值即可得解;
的最小值即可得解;
(Ⅱ)结合(Ⅰ)中函数的单调性只需讨论![]() 时,通过讨论导数的正负得
时,通过讨论导数的正负得![]() 使得
使得![]() ,
,![]() 使得
使得![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增,所以
上单调递增,所以![]() ,结合
,结合![]() ,消去
,消去![]() 留
留![]() ,构造
,构造![]() ,可证得
,可证得![]() ,进而只需证明
,进而只需证明![]() ,再构造函数利用单调性即可证得.
,再构造函数利用单调性即可证得.
(Ⅰ)由题意知![]() ,
,
令![]() ,
,![]() ,
,
显然![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
故当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以![]() .
.
若![]() 为增函数,则
为增函数,则![]() 恒成立,即
恒成立,即![]() ,即
,即![]() .
.
经检验,当![]() 时,满足题意.
时,满足题意.
(Ⅱ)由(Ⅰ)知![]() 时,
时,![]() 为增函数,不存在极小值;
为增函数,不存在极小值;
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
故存在![]() 使得
使得![]() ;
;
![]() ,令
,令![]() ,
,![]() ,
,
显然![]() 在
在![]() 上单调递增,
上单调递增,
故![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
故![]() ,故
,故![]() ,
,
因此存在![]() 使得
使得![]() .
.
因此![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增.
上单调递增.
![]() ,
,![]() ,
,
由![]() 代入消去
代入消去![]() 得
得![]() ,
,
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
故![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
即![]() 在
在![]() 上单调递减,故
上单调递减,故![]() ,
,
故要证![]() ,只需证
,只需证![]() ,
,
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
故当![]() 时,
时,![]() .
.
综上,![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,且asinB![]() bcosA+a=bcosC+ccosB.
bcosA+a=bcosC+ccosB.
(1)求A;
(2)若a![]() ,点D在BC上,且AD⊥AC,当△ABC的周长取得最大值时,求BD的长.
,点D在BC上,且AD⊥AC,当△ABC的周长取得最大值时,求BD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() ,设直线
,设直线![]() 经过点
经过点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 两点,抛物线
两点,抛物线![]() 在
在![]() 、
、![]() 两点处的切线相交于点
两点处的切线相交于点![]() ,直线
,直线![]() ,
,![]() 分别与
分别与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.

(1)求点![]() 的轨迹方程
的轨迹方程
(2)当点![]() 不在
不在![]() 轴上时,记
轴上时,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象如图所示,给出四个函数:①
的图象如图所示,给出四个函数:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,又给出四个函数的图象,则正确的匹配方案是( ).
,又给出四个函数的图象,则正确的匹配方案是( ).
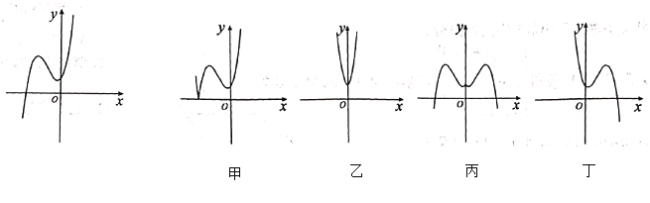
A.①-甲,②-乙,③-丙,④-丁B.②-甲,①-乙,③-丙,④-丙
C.①-甲,③-乙,④-丙,②-丁D.①-甲,④-乙,③-丙,②-丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】采购经理指数(PMⅠ)是衡量一个国家制造业的“体检表”,是衡量制造业在生产、新订单、商品价格、存货、雇员、订单交货新出口订单和进口等八个方面状况的指数,图为2018年9月—2019年9月我国制造业的采购经理指数(单位:%).
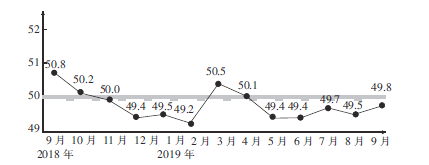
(1)求2019年前9个月我国制造业的采购经理指数的平均数(精确到0.1);
(2)从2018年10月—2019年9月这12个月任意选取4个月,记采购经理指数与上个月相比有所回升的月份个数为X,求X的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的普通方程;
的普通方程;
(2)设![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com