
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
【答案】(1)![]() (2)m≤﹣
(2)m≤﹣![]() 或m≥1.
或m≥1.
【解析】试题分析:(Ⅰ)分三种情况讨论,分别求解不等式组,然后求并集即可得结果;(Ⅱ)原不等式等价于f(x)min≤|3m+1|,求出![]() 的最小值,解关于
的最小值,解关于![]() 的不等式,即可得结果.
的不等式,即可得结果.
试题解析:解:(Ⅰ)不等式f(x)<8,即|2x+3|+|2x﹣1|<8,
可化为①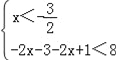 或②
或②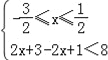 或③
或③ ,…
,…
解①得﹣![]() <x<﹣
<x<﹣![]() ,解②得﹣
,解②得﹣![]() ≤x≤
≤x≤![]() ,解③得
,解③得![]() <x<
<x<![]() ,
,
综合得原不等式的解集为{x|-![]() }.
}.
(Ⅱ)因为∵f(x)=|2x+3|+|2x﹣1|≥|(2x+3)﹣(2x﹣1)|=4,
当且仅当﹣![]() ≤x≤
≤x≤![]() 时,等号成立,即f(x)min=4,…
时,等号成立,即f(x)min=4,…
又不等式f(x)≤|3m+1|有解,则|3m+1|≥4,解得:m≤﹣![]() 或m≥1.
或m≥1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知坐标平面上点![]() 与两个定点
与两个定点![]() ,
, ![]() 的距离之比等于5.
的距离之比等于5.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段的长为 8,求直线
所截得的线段的长为 8,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:指数函数f(x)=(2a-6)x在R上是单调减函数;q:关于x的方程x2-3ax+2a2+1=0的两根均大于3,若p或q为真,p且q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题,其中正确的序号是__________________(写出所有正确命题的序号)
①函数![]() 的图像恒过定点
的图像恒过定点![]() ;
;
②已知集合![]() ,则映射
,则映射![]() 中满足
中满足![]() 的映射共有1个;
的映射共有1个;
③若函数![]() 的值域为R,则实数
的值域为R,则实数![]() 的取值范围是
的取值范围是![]() ;
;
④函数![]() 的图像关于
的图像关于![]() 对称的函数解析式为
对称的函数解析式为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数![]() 是奇函数
是奇函数
(1)求![]() 的值
的值
(2)判断f(x)在![]() 上的单调性。(直接写出答案,不用证明)
上的单调性。(直接写出答案,不用证明)
(3)若对于任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-1|+|x+1|(x∈R).
(1)证明:函数f(x)是偶函数;
(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图象;
(3)写出函数的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】罗源滨海新城建一座桥,两端的桥墩已建好,这两墩相距![]() 米,余下工程只需建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为32万元,距离为x米的相邻两墩之间的桥面工程费用为
米,余下工程只需建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为32万元,距离为x米的相邻两墩之间的桥面工程费用为![]() 万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为![]() 万元.
万元.
(1)试写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() =96米,需新建多少个桥墩才能使余下工程的费用
=96米,需新建多少个桥墩才能使余下工程的费用![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
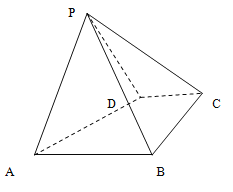
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,且
,且![]() 是以
是以![]() 为底的等腰三角形.
为底的等腰三角形.
(Ⅰ)证明:![]()
(Ⅱ)若四棱锥![]() 的体积等于
的体积等于![]() .问:是否存在过点
.问:是否存在过点![]() 的平面
的平面![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com