
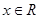 ,
, 恒成立(其中
恒成立(其中 ),求
),求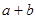 的最大值.
的最大值.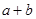 的最大值为
的最大值为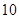 .
.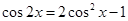 ,利用换元法
,利用换元法 ,将原不等式转化为二次不等式
,将原不等式转化为二次不等式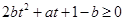 在区间
在区间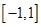 上恒成立,利用二次函数的零点分布进行讨论,从而得出
上恒成立,利用二次函数的零点分布进行讨论,从而得出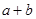 的最大值,但是在对
的最大值,但是在对 时的情况下,主要对二次函数的对称轴
时的情况下,主要对二次函数的对称轴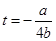 是否在区间
是否在区间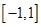 进行分类讨论,再将问题转化为
进行分类讨论,再将问题转化为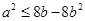 的条件下,求
的条件下,求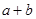 的最大值,
的最大值,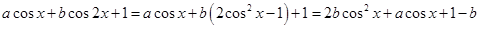 ,
,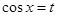 ,
,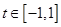 ,则当
,则当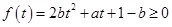 ,
,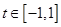 恒成立,开口向上,
恒成立,开口向上,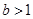 时,
时,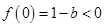 ,不满足
,不满足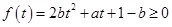 ,
,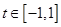 恒成立,
恒成立, 时,则必有
时,则必有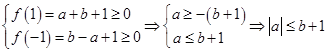 (1)
(1)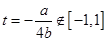 时,即
时,即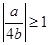 ,也即
,也即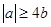 时,有
时,有 ,
,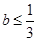 ,
,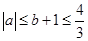 ,则
,则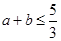 ,当
,当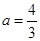 ,
,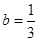 时,
时,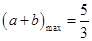 .
.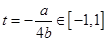 时,即
时,即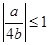 ,也即
,也即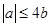 时,
时,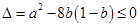 ,即
,即 ,又由(1)知
,又由(1)知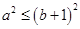 ,
,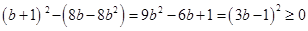 ,故只需
,故只需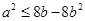 成立即可,
成立即可,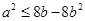 的条件下,求
的条件下,求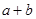 的最大值,然后利用代数式的结构特点或从题干中的式子出发,分别利用三角换元法、导数法以及柯西不等式法来求
的最大值,然后利用代数式的结构特点或从题干中的式子出发,分别利用三角换元法、导数法以及柯西不等式法来求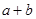 的最大值.
的最大值.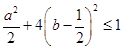 ,
,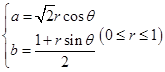 ,所以
,所以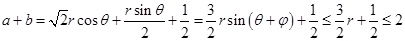 ,
,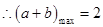 ;
;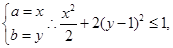 则即求函数的导数,椭圆的上半部分
则即求函数的导数,椭圆的上半部分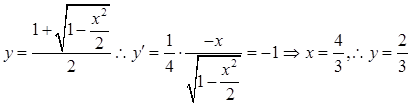
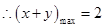 ;
;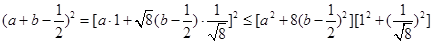
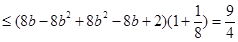 ,当且仅当
,当且仅当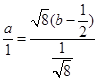 ,即
,即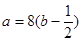 及
及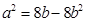 时等号成立.即当
时等号成立.即当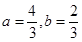 时,
时,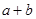 最大值为2.
最大值为2.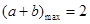 .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:不详 题型:解答题
| ||
| 2 |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com