
设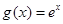 ,
, ,其中
,其中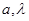 是常数,且
是常数,且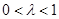 .
.
(1)求函数 的极值;
的极值;
(2)证明:对任意正数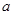 ,存在正数
,存在正数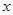 ,使不等式
,使不等式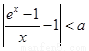 成立;
成立;
(3)设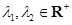 ,且
,且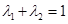 ,证明:对任意正数
,证明:对任意正数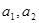 都有:
都有: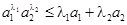 .
.
(1) 当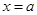 时,
时,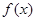 取极大值,但
取极大值,但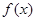 没有极小值;(2)详见解析;(3)详见解析.
没有极小值;(2)详见解析;(3)详见解析.
【解析】
试题分析:(1)先求导,再讨论函数的单调区间,然后写出函数的极值;(2)通过依次构造函数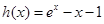 、
、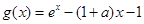 和
和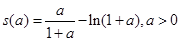 ,利用导数来研究其单调性和最值情况,从而用来比较大小,最终达到证明不等式的目的; (3)先把所要证明的不等式的左边转变到函数
,利用导数来研究其单调性和最值情况,从而用来比较大小,最终达到证明不等式的目的; (3)先把所要证明的不等式的左边转变到函数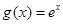 的问题,得到相关的不等式
的问题,得到相关的不等式 ,再借助(1)中
,再借助(1)中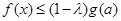 的结论得到
的结论得到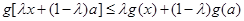 ,最后取
,最后取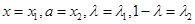 即可证得.
即可证得.
试题解析:(1)∵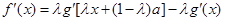 ,
1分
,
1分
由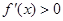 得,
得,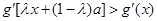 ,
,
∴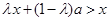 ,即
,即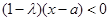 ,解得
,解得 , 3分
, 3分
故当 时,
时,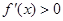 ;当
;当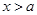 时,
时,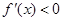 ;
;
∴当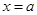 时,
时,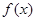 取极大值,但
取极大值,但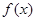 没有极小值. 4分
没有极小值. 4分
(2)∵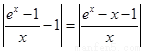 ,又当
,又当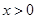 时,令
时,令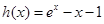 ,则
,则
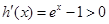 ,
,
故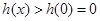 ,因此原不等式化为
,因此原不等式化为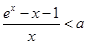 ,即
,即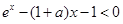 ,
,
令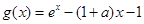 ,则
,则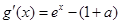 ,
,
由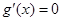 得:
得: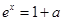 ,解得
,解得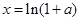 ,
,
当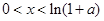 时,
时,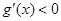 ;当
;当 时,
时,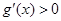 .
.
故当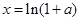 时,
时,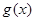 取最小值
取最小值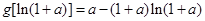 , 8分
, 8分
令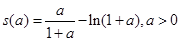 ,则
,则 .
.
故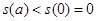 ,即
,即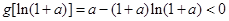 .
.
因此,存在正数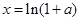 ,使原不等式成立. 10分
,使原不等式成立. 10分
(3)对任意正数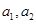 ,存在实数
,存在实数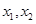 使
使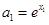 ,
,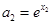 ,
,
则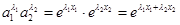 ,
,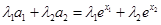 ,
,
原不等式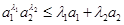
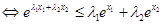 ,
,
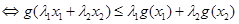 12分
12分
由(1)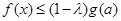 恒成立,故
恒成立,故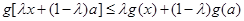 ,
,
取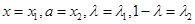 ,即得
,即得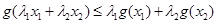 ,
,
即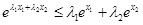 ,故所证不等式成立. 14分
,故所证不等式成立. 14分
考点:1、导数的应用,2、函数单调性的应用,3、不等式的证明.


科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
| 3π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| x+1 |
| 1 |
| |P1P2|2 |
| 1 |
| |P1P3|2 |
| 1 |
| |P1Pn|2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:2007-2008学年北京市西城区高一(上)期末数学试卷(解析版) 题型:解答题
 .先把y=f(x)的图象上所有点向左平移
.先把y=f(x)的图象上所有点向左平移 个单位长度,再把所得图象上所有点的横坐标缩短到原来的
个单位长度,再把所得图象上所有点的横坐标缩短到原来的 (纵坐标不变)得到函数y=g(x)的图象.
(纵坐标不变)得到函数y=g(x)的图象.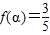 ,
,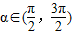 ,求f(2α)的值;
,求f(2α)的值;查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三12月月考理科数学试卷 题型:解答题
某唱片公司要发行一张名为《春风再美也比不上你的笑》的唱片,包含《新花好月圆》、《荷塘月色》等10首创新经典歌曲。该公司计划用 (百万元)请李子恒老师进行创作,经调研知:该唱片的总利润
(百万元)请李子恒老师进行创作,经调研知:该唱片的总利润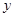 (百万元)与
(百万元)与 成正比的关系,当
成正比的关系,当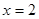 时
时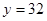 .又有
.又有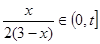 ,其中
,其中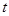 是常数,且
是常数,且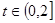 .
.
(Ⅰ)设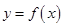 ,求其表达式,定义域(用
,求其表达式,定义域(用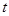 表示);
表示);
(Ⅱ)求总利润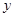 的最大值及相应的
的最大值及相应的 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com