
分析 ①利用余弦定理,即可求出角B的大小;
②利用正弦定理求出c=4sinC,从而写出$\overrightarrow{AB}$$•\overrightarrow{AC}$,再利用三角恒等变换以及角C的取值范围,求出$\overrightarrow{AB}$•$\overrightarrow{AC}$的最大值.
解答 解:①△ABC中,a2+c2=b2+ac,
∴a2+c2-b2=ac,
∴cosB=$\frac{{a}^{2}{+c}^{2}{-b}^{2}}{2ac}$=$\frac{1}{2}$,
又B∈(0°,180°),
∴B=60°;
②由AC=b=2$\sqrt{3}$,
∴$\frac{c}{sinC}$=$\frac{b}{sinB}$=$\frac{2\sqrt{3}}{sin60°}$=4,
∴c=4sinC;
∴$\overrightarrow{AB}$$•\overrightarrow{AC}$=cb•cosA
=2$\sqrt{3}$c•cosA
=2$\sqrt{3}$×4sinC•cosA
=8$\sqrt{3}$sinCcos(120°-C)
=8$\sqrt{3}$sinC(-$\frac{1}{2}$cosC+$\frac{\sqrt{3}}{2}$sinC)
=-4$\sqrt{3}$sinCcosC+12sin2C
=-2$\sqrt{3}$sin2C+12×$\frac{1-cos2C}{2}$
=-2$\sqrt{3}$sin2C-6cos2C+6
=-4$\sqrt{3}$($\frac{1}{2}$sin2C+$\frac{\sqrt{3}}{2}$cos2C)+6
=-4$\sqrt{3}$sin(2C+60°)+6;
又C∈(0°,120°),
∴2C+60°∈(60°,300°),
∴当2C+60°=270°,即C=105°时,
$\overrightarrow{AB}$•$\overrightarrow{AC}$取得最大值为-4$\sqrt{3}$×(-1)+6=4$\sqrt{3}$+6.
故答案为:60°,4$\sqrt{3}$+6.
点评 本题考查了正弦、余弦定理的应用问题,也考查了三角恒等变换的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
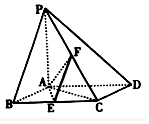 如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.
如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
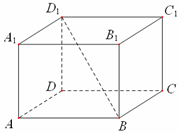 如图,在正四棱柱ABCD-A1B1C1D1中,底面ABCD的边长为7,BD1与底面所成角的大小为$arctan\frac{6}{7}$,则该正四棱柱的高等于$6\sqrt{2}$.
如图,在正四棱柱ABCD-A1B1C1D1中,底面ABCD的边长为7,BD1与底面所成角的大小为$arctan\frac{6}{7}$,则该正四棱柱的高等于$6\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或2 | B. | 2 | C. | 1 | D. | 1或-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.45 | B. | 0.5 | C. | 0.55 | D. | 0.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a>b,则ac>bc”是真命题 | |
| B. | 命题“若a2+b2=0,则a,b全为0”是真命题 | |
| C. | 命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0” | |
| D. | 命题“若a=0,则ab=0”的逆否命题是“若ab≠0,则a≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
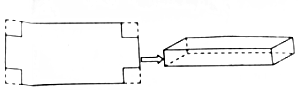 如图,在一张长为2a米,宽为a米(a>2)的矩形铁皮的四个角上,各剪去一个边长是x米(0<x≤1)的小正方形,折成一个无盖的长方体铁盒,设V(x)表示铁盒的容积.
如图,在一张长为2a米,宽为a米(a>2)的矩形铁皮的四个角上,各剪去一个边长是x米(0<x≤1)的小正方形,折成一个无盖的长方体铁盒,设V(x)表示铁盒的容积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com