
【题目】在棱长为1的正方体![]() 中,MN分别是棱
中,MN分别是棱![]() 的中点,P是体对角线
的中点,P是体对角线![]() 上一点,满足
上一点,满足![]() ,则平面MNP截正方体所得截面周长为_______
,则平面MNP截正方体所得截面周长为_______
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,
,![]() .
.
(1)若![]() ,且点
,且点![]() 满足
满足![]() ,证明:点
,证明:点![]() 不在椭圆
不在椭圆![]() 上;
上;
(2)若椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,直线
,直线![]() 与线段
与线段![]() 和椭圆
和椭圆![]() 的短轴分别交于两个不同点
的短轴分别交于两个不同点![]() ,
,![]() ,且
,且![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出有关![]() 的四个论断:①
的四个论断:①![]() ;②
;②![]() ;③
;③![]() 或
或![]() ;④
;④![]() .以其中的三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:若______,则_______(用序号表示)并给出证明过程:
.以其中的三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:若______,则_______(用序号表示)并给出证明过程:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点![]() 的距离之比为定值
的距离之比为定值![]() 的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系
的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系![]() 中,
中,![]() 点
点![]() .设点
.设点![]() 的轨迹为
的轨迹为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A. ![]() 的方程为
的方程为![]()
B. 在![]() 轴上存在异于
轴上存在异于![]() 的两定点
的两定点![]() ,使得
,使得![]()
C. 当![]() 三点不共线时,射线
三点不共线时,射线![]() 是
是![]() 的平分线
的平分线
D. 在![]() 上存在点
上存在点![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某区有一块空地![]() ,其中
,其中![]() ,
,![]() ,
,![]() .当地区政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖
.当地区政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖![]() ,其中
,其中![]() 都在边
都在边![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地带上形成假山,剩下的
地带上形成假山,剩下的![]() 地带开设儿童游乐场.为安全起见,需在
地带开设儿童游乐场.为安全起见,需在![]() 的周围安装防护网.
的周围安装防护网.

(1)当![]() 时,求防护网的总长度;
时,求防护网的总长度;
(2)若要求挖人工湖用地![]() 的面积是堆假山用地
的面积是堆假山用地![]() 的面积的
的面积的![]() 倍,试确定
倍,试确定![]() 的大小;
的大小;
(3)为节省投入资金,人工湖![]() 的面积要尽可能小,问如何设计施工方案,可使
的面积要尽可能小,问如何设计施工方案,可使![]() 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: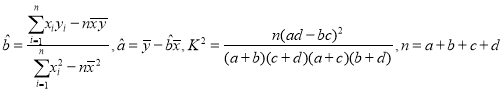 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在坐标原点,准线方程为
的顶点在坐标原点,准线方程为![]() ,
,![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 为直线
为直线![]() 上任意一点,以
上任意一点,以![]() 为圆心,
为圆心,![]() 为半径的圆与抛物线
为半径的圆与抛物线![]() 的准线交于
的准线交于![]() 、
、![]() 两点,过
两点,过![]() 、
、![]() 分别作准线的垂线交抛物线
分别作准线的垂线交抛物线![]() 于点
于点![]() 、
、![]() .
.
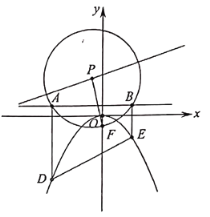
(1)求抛物线![]() 的方程;
的方程;
(2)证明:直线![]() 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com