
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,
,![]() .
.
(1)若![]() ,且点
,且点![]() 满足
满足![]() ,证明:点
,证明:点![]() 不在椭圆
不在椭圆![]() 上;
上;
(2)若椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,直线
,直线![]() 与线段
与线段![]() 和椭圆
和椭圆![]() 的短轴分别交于两个不同点
的短轴分别交于两个不同点![]() ,
,![]() ,且
,且![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左,右焦点,
的左,右焦点,![]() 两点分别是椭圆
两点分别是椭圆![]() 的上,下顶点,
的上,下顶点,![]() 是等腰直角三角形,延长
是等腰直角三角形,延长![]() 交椭圆
交椭圆![]() 于
于![]() 点,且
点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,直线
的动点,直线![]() 与直
与直![]() 分别相交于
分别相交于![]() 两点,点
两点,点![]() ,求证:
,求证:![]() 的外接圆恒过原点
的外接圆恒过原点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗失眠症的药(分别称为![]() 药,
药,![]() 药)的疗效,某机构随机地选取
药)的疗效,某机构随机地选取![]() 位患者服用
位患者服用![]() 药,
药,![]() 位患者服用
位患者服用![]() 药,观察这
药,观察这![]() 位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:
位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:![]() ),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:
),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:
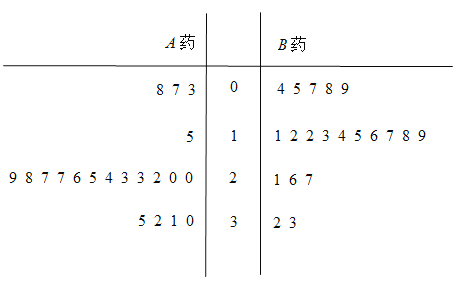
(1)根据茎叶图判断哪种药对增加睡眠时间更有效?并说明理由;
(2)求这![]() 名患者日平均增加睡眠时间的中位数
名患者日平均增加睡眠时间的中位数![]() ,并将日平均增加睡眠时间超过
,并将日平均增加睡眠时间超过![]() 和不超过
和不超过![]() 的患者人数填入下面的列联表:
的患者人数填入下面的列联表:
超过 | 不超过 | |
服用 | ||
服用 |
(3)根据(2)中的列联表,能否有![]() 的把握认为
的把握认为![]() 两种药的疗效有差异?
两种药的疗效有差异?
附: 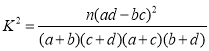 .
.
| 0.01 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为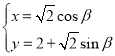 (
(![]() 为参数),直线
为参数),直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,以原点为极点,
,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)若相交于不同的两点![]() ,求
,求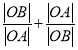 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系![]() 的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线
的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线![]() (
(![]() 为参数)上每一点的横坐标变为原来的
为参数)上每一点的横坐标变为原来的![]() (纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为
(纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为![]() .
.
(1)求曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,与x轴交于点P,线段AB的中点为M,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com