
【题目】为了比较两种治疗失眠症的药(分别称为![]() 药,
药,![]() 药)的疗效,某机构随机地选取
药)的疗效,某机构随机地选取![]() 位患者服用
位患者服用![]() 药,
药,![]() 位患者服用
位患者服用![]() 药,观察这
药,观察这![]() 位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:
位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:![]() ),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:
),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:
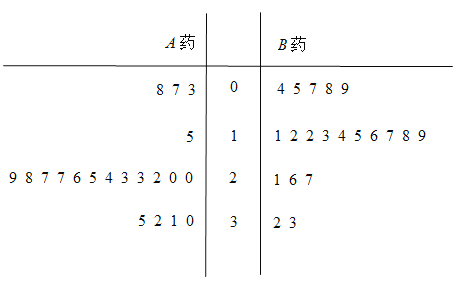
(1)根据茎叶图判断哪种药对增加睡眠时间更有效?并说明理由;
(2)求这![]() 名患者日平均增加睡眠时间的中位数
名患者日平均增加睡眠时间的中位数![]() ,并将日平均增加睡眠时间超过
,并将日平均增加睡眠时间超过![]() 和不超过
和不超过![]() 的患者人数填入下面的列联表:
的患者人数填入下面的列联表:
超过 | 不超过 | |
服用 | ||
服用 |
(3)根据(2)中的列联表,能否有![]() 的把握认为
的把握认为![]() 两种药的疗效有差异?
两种药的疗效有差异?
附: 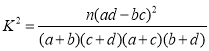 .
.
| 0.01 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【答案】(1)![]() 药的疗效更好.(2)
药的疗效更好.(2)![]() ,见解析(3)有
,见解析(3)有
【解析】
(1)根据茎叶图中叶的集中情况、平均数、中位数和茎的对称分布,即可分析出![]() 药的疗效更好;
药的疗效更好;
(2)由茎叶图可知,![]() 组数据的中位数为
组数据的中位数为![]() ,即可得出
,即可得出![]() 药和
药和![]() 药中超过和不超过2的人数,即可填出列联表;
药中超过和不超过2的人数,即可填出列联表;
(3)根据列联表,求出![]() ,与临界值
,与临界值![]() 比较,即可得出结论.
比较,即可得出结论.
解:(1)①从以上茎叶图可以看出,![]() 药疗效的试验结果有
药疗效的试验结果有![]() 的叶集中在茎
的叶集中在茎![]() 和
和![]() 上,
上,
而![]() 药疗效的试验结果有
药疗效的试验结果有![]() 的叶集中在茎
的叶集中在茎![]() 和
和![]() 上,由此可看出
上,由此可看出![]() 药的疗效更好;
药的疗效更好;
②从茎叶图的分布情况可以看出,服用![]() 药的患者日平均增加睡眠时间的平均数大于
药的患者日平均增加睡眠时间的平均数大于![]() ,
,
而服用![]() 药的患者日平均增加睡眠时间的平均数小于
药的患者日平均增加睡眠时间的平均数小于![]() ,因此可知
,因此可知![]() 药的疗效更好;
药的疗效更好;
③由茎叶图可知,服用![]() 药的患者日平均增加睡眠时间的中位数是
药的患者日平均增加睡眠时间的中位数是![]() ,
,
而服用![]() 药的患者日平均增加睡眠时间的中位数是
药的患者日平均增加睡眠时间的中位数是![]() ,因此
,因此![]() 药的疗效更好;
药的疗效更好;
④由茎叶图可知,服用![]() 药的患者日平均增加睡眠时间分布在茎
药的患者日平均增加睡眠时间分布在茎![]() 上的最多,关于茎
上的最多,关于茎![]() 大致呈对称分布,
大致呈对称分布,
而服用![]() 药的患者日平均增加睡眠时间分布在茎
药的患者日平均增加睡眠时间分布在茎![]() 上的最多,关于茎
上的最多,关于茎![]() 大致呈对称分布,
大致呈对称分布,
又患者在服用两种药后日平均增加睡眠时间分布的区间相同,
故可以认为服用![]() 药的患者日平均增加睡眠时间比服用
药的患者日平均增加睡眠时间比服用![]() 药的患者日平均增加睡眠时间更多,
药的患者日平均增加睡眠时间更多,
因此![]() 药的疗效更好.
药的疗效更好.
(2)由茎叶图可知,![]() 组数据的中位数为
组数据的中位数为![]() ,
,
因此可得列联表如下:
超过 | 不超过 | |
服用 | 14 | 6 |
服用 | 5 | 15 |
(3)由于![]() ,
,
所以有![]() 的把握认为
的把握认为![]() 两种药的疗效有差异.
两种药的疗效有差异.


科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() ,若点
,若点![]() 为抛物线
为抛物线![]() 准线上的动点,给出以下命题:
准线上的动点,给出以下命题:
①当![]() 为正三角形时,
为正三角形时,![]() 的值为
的值为![]() ;
;
②存在![]() 点,使得
点,使得![]() ;
;
③若![]() ,则
,则![]() 等于
等于![]() ;
;
④![]() 的最小值为
的最小值为![]() ,则
,则![]() 等于
等于![]() 或
或![]() .
.
其中正确的是( )
A.①③④B.②③C.①③D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形![]() 为菱形,且
为菱形,且![]() ,取
,取![]() 中点为
中点为![]() .现将四边形
.现将四边形![]() 沿
沿![]() 折起至
折起至![]() ,使得
,使得![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 满足
满足![]() ,当
,当![]() 平面
平面![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了推进分级诊疗,实现“基层首诊、双向转诊、急慢分治、上下联动”的诊疗模式,某地区自2016年起全面推行家庭医生签约服务.已知该地区居民约为2000万,从1岁到101岁的居民年龄结构的频率分布直方图如图1所示.为了解各年龄段居民签约家庭医生的情况,现调查了1000名年满18周岁的居民,各年龄段被访者签约率如图2所示.
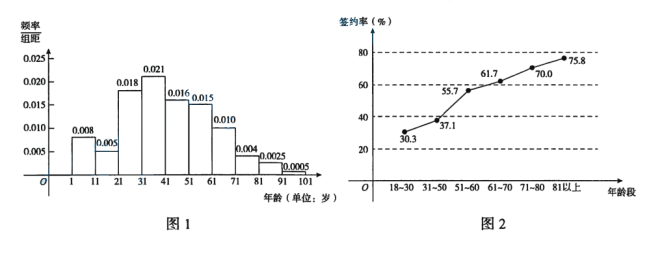
(1)估计该地区年龄在71~80岁且已签约家庭医生的居民人数;
(2)若以图2中年龄在71~80岁居民签约率作为此地区该年龄段每个居民签约家庭医生的概率,则从该地区年龄在71~80岁居民中随机抽取两人,求这两人中恰有1人已签约家庭医生的概率;
(3)据统计,该地区被访者的签约率约为![]() .为把该地区年满18周岁居民的签约率提高到
.为把该地区年满18周岁居民的签约率提高到![]() 以上,应着重提高图2中哪个年龄段的签约率?并结合数据对你的结论作出解释.
以上,应着重提高图2中哪个年龄段的签约率?并结合数据对你的结论作出解释.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非典和新冠肺炎两场疫情告诉我们:应坚决杜绝食用野生动物,提倡文明健康,绿色环保的生活方式.在我国抗击新冠肺炎期间,某校开展一次有关病毒的网络科普讲座.高三年级男生60人,女生40人参加.按分层抽样的方法,在100名同学中选出5人,则男生中选出________人.再从此5人中选出两名同学作为联络人,则这两名联络人中男女都有的概率是________.(第1空2分,第2空3分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,
,![]() .
.
(1)若![]() ,且点
,且点![]() 满足
满足![]() ,证明:点
,证明:点![]() 不在椭圆
不在椭圆![]() 上;
上;
(2)若椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,直线
,直线![]() 与线段
与线段![]() 和椭圆
和椭圆![]() 的短轴分别交于两个不同点
的短轴分别交于两个不同点![]() ,
,![]() ,且
,且![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.对于n∈N*(n≥2),定义一个如下数阵: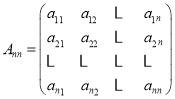 ,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设
,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设![]() .
.
(Ⅰ)当n=6时,试写出数阵A66并计算![]() ;
;
(Ⅱ)若[x]表示不超过x的最大整数,求证:![]() ;
;
(Ⅲ)若![]() ,
,![]() ,求证:g(n)﹣1<f(n)<g(n)+1.
,求证:g(n)﹣1<f(n)<g(n)+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出有关![]() 的四个论断:①
的四个论断:①![]() ;②
;②![]() ;③
;③![]() 或
或![]() ;④
;④![]() .以其中的三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:若______,则_______(用序号表示)并给出证明过程:
.以其中的三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:若______,则_______(用序号表示)并给出证明过程:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com