
分析 (Ⅰ)B点坐标为$(-\frac{3}{5},\frac{4}{5})$时,可画出图形,从而可得出sinθ,cosθ的值,进而得出tanθ的值,这样根据两角差的正切公式便可求出$tan(\frac{π}{4}-θ)$的值;
(Ⅱ)根据条件可得到$\overrightarrow{OA}=(2,0),\overrightarrow{OB}=(cosθ,sinθ)$,从而可表示出$\overrightarrow{OC}$的坐标,进行数量积的坐标运算便可由$\overrightarrow{OB}•\overrightarrow{OC}=\frac{23}{13}$得出cosθ的值,进而求出sinθ的值,从而便可求出$cos(\frac{π}{3}+θ)$的值.
解答 解:(Ⅰ)若$B(-\frac{3}{5},\frac{4}{5})$,如图: 则:
则:
$sinθ=\frac{4}{5},cosθ=-\frac{3}{5}$;
∴$tanθ=-\frac{4}{3}$;
∴$tan(\frac{π}{4}-θ)=\frac{1-tanθ}{1+tanθ}=\frac{1-(-\frac{4}{3})}{1+(-\frac{4}{3})}=-7$;
(Ⅱ)$\overrightarrow{OA}=(2,0),\overrightarrow{OB}=(cosθ,sinθ)$;
∴$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}=(2+cosθ,sinθ)$;
∴$\overrightarrow{OB}•\overrightarrow{OC}=cosθ(2+cosθ)+si{n}^{2}θ$=$2cosθ+1=\frac{23}{13}$;
∴$cosθ=\frac{5}{13}$;
又θ∈(0,π);
∴$sinθ=\frac{12}{13}$;
∴$cos(\frac{π}{3}+θ)=cos\frac{π}{3}cosθ-sin\frac{π}{3}sinθ$
=$\frac{1}{2}×\frac{5}{13}-\frac{\sqrt{3}}{2}×\frac{12}{13}$
=$\frac{5-12\sqrt{3}}{26}$.
点评 考查单位圆的概念,以及三角函数的定义,弦化切公式,两角差的正切公式,两角和的余弦公式,以及根据点的坐标求向量坐标,向量坐标的加法和数量积运算.


科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | 5 | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x2 | B. | y=x-1 | C. | y=x${\;}^{\frac{1}{2}}$ | D. | y=x3-x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{11}{8}$ | D. | $-\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
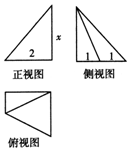
| A. | $\frac{5}{6}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{4}{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com