
在△ABC中,角A,B,C所对的边分别为a,b,c且满足c sinA=a cosC.
(1)求角C的大小;
(2)求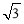 sinA –cos(B+C)的取值范围.
sinA –cos(B+C)的取值范围.
(1)C=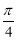 ;(2)
;(2)
【解析】
试题分析:(1)由正弦定理得sinCsinA=sinAcosC , 所以tanC=1,则C=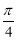
(2)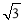 sinA –cos(B+C)=
sinA –cos(B+C)= 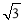 sinA –cos(
sinA –cos( -A )
-A )
=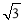 sinA –cosA=2sin(A+
sinA –cosA=2sin(A+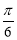 )
)
又 0 < A< 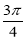 ,
, 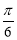 < A+
< A+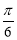 <
<  ,
,
所以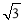 sinA –cos(B+C) 的取值范围
sinA –cos(B+C) 的取值范围
试题解析:(1)已知c sinA=a cosC
由正弦定理得sinCsinA=sinAcosC ,
因为0<A< , 所以sinA>0, 得sinC=cosC ,
, 所以sinA>0, 得sinC=cosC ,
又cosC ≠0,所以tanC=1,则C=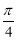
(2)已知A+B+C=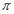 ,所以
,所以
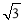 sinA –cos(B+C)=
sinA –cos(B+C)= 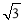 sinA –cos(
sinA –cos( -A ) =
-A ) =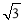 sinA –cosA=2sin(A+
sinA –cosA=2sin(A+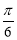 )
)
又C=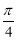 ,所以0 < A<
,所以0 < A< 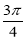 ,
, 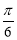 < A+
< A+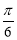 <
<  ,
,
所以sin(A+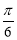 )
) ,
,
所以2sin(A+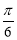 )
)
综上所述,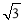 sinA –cos(B+C) 的取值范围
sinA –cos(B+C) 的取值范围
考点:正弦定理,三角函数恒等变换.


科目:高中数学 来源:2016届河北省承德市联校高一下学期期末考试数学试卷(解析版) 题型:解答题
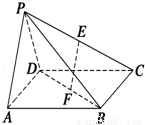
如图,在四棱锥P﹣ABCD中,底面ABCD是边长为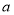 的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=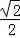 AD.
AD.
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源:2016届江西省高一下学期第二次月考数学试卷(解析版) 题型:选择题
设等差数列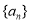 的公差d不为0,
的公差d不为0,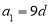 ,若
,若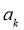 是
是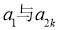 的等比中项,则k=( )
的等比中项,则k=( )
A.2 B.6 C. 8 D.4
查看答案和解析>>
科目:高中数学 来源:2016届江西省高一下学期第二次段考数学试卷(解析版) 题型:选择题
命题:公差不为0的等差数列的通项可以表示为关于n的一次函数形式,反之通项是关于n的一次函数形式的数列为等差数列为真,现有正项数列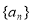 的前n项和是Sn,若
的前n项和是Sn,若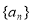 和
和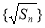 都是等差数列,且公差相等,则数列
都是等差数列,且公差相等,则数列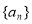 的一个通项公式为( ).
的一个通项公式为( ).
A.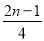 B.
B.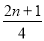 C.
C.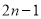 D.
D.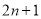
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com