
分析 (Ⅰ)当n=2时,由平方关系求得f(α)=1,得到f(α)的值域为{1};当n=4时,把f(α)变形可得f(α)=$1-\frac{1}{2}si{n}^{2}2α$,得f(α)的值域为[$\frac{1}{2}$,1];当n=6时,f(α)=$1-\frac{3}{4}si{n}^{2}2α$,f(α)的值域为[$\frac{1}{4}$,1].
(Ⅱ)由(Ⅰ)的结论猜想,当n=2k,k∈N*时,$\frac{1}{{2}^{k-1}}≤f(α)≤1$.
解答 解:(Ⅰ)当n=2时,f(α)=sin2α+cos2α=1,∴f(α)的值域为{1};
当n=4时,f(α)=sin4α+cos4α=$(si{n}^{2}α+co{s}^{2}α)^{2}-2si{n}^{2}αco{s}^{2}α=1-\frac{1}{2}si{n}^{2}2α$,
此时有$\frac{1}{2}≤$f(α)≤1,∴f(α)的值域为[$\frac{1}{2}$,1];
当n=6时,f(α)=sin6α+cos6α=(sin2α+cos2α)(sin4α+cos4α-sin2αcos2α)
=$1-3si{n}^{2}αco{s}^{2}α=1-\frac{3}{4}si{n}^{2}2α$,
此时有$\frac{1}{4}≤$f(α)≤1,∴f(α)的值域为[$\frac{1}{4}$,1].
(Ⅱ)由以上结论猜想,当n=2k,k∈N*时,$\frac{1}{{2}^{k-1}}≤f(α)≤1$.
点评 本题考查三角函数最值的求法,考查三角函数的值域,训练了同角三角函数基本关系式的应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
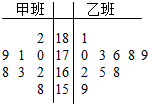 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图示,根据茎叶图解答下列问题;
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图示,根据茎叶图解答下列问题;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-,+∞) | B. | (-1,2) | C. | {y|y≠2} | D. | {y|y>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
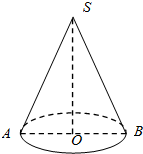 如图,在圆锥SO中,其母线长为2,底面半径为$\frac{1}{2}$,一只虫子从底面圆周上一点A出发沿圆锥表面爬行一周后又回到A点,则这只虫子所爬过的最短路程是2$\sqrt{2}$.
如图,在圆锥SO中,其母线长为2,底面半径为$\frac{1}{2}$,一只虫子从底面圆周上一点A出发沿圆锥表面爬行一周后又回到A点,则这只虫子所爬过的最短路程是2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com