
【题目】已知动直线l过抛物线C:y2=4x的焦点F,且与抛物线C交于M,N两点,且点M在x轴上方.
(1)若线段MN的垂直平分线交x轴于点Q,若|FQ|=8,求直线l的斜率;
(2)设点P(x0,0),若点M恒在以FP为直径的圆外,求x0的取值范围.
【答案】(1)![]() ;(2)x0∈[0,1)∪(1,9).
;(2)x0∈[0,1)∪(1,9).
【解析】
(1)由题意可得直线l的斜率存在且不为0,设l的方程与抛物线联立,求出两根之和及两根之积,进而可得MN的中点坐标,进而可得MN的中垂线方程,令y=0可得Q的坐标,进而求出|QF|的值,由题意可得直线l的斜率;
(2)由题意可得∠FMP为锐角,等价于![]() 0,求出
0,求出![]() 的表达式,换元等价于h(t)=t2+(3﹣x0)4+x0,t>0恒成立,分两种情况求出x0 取值范围.
的表达式,换元等价于h(t)=t2+(3﹣x0)4+x0,t>0恒成立,分两种情况求出x0 取值范围.
(1)由题意可得直线l的斜率存在且不为0,设直线l的方程为:x=ty+1,设M(x1,y1),N(x2,y2),线段MN的最大E(x0,y0),
联立直线与抛物线的方程可得:![]() ,
,
整理可得y2﹣4ty﹣4=0,
所以y1+y2=4t,y1y2=﹣4,
所以y0=2t,x0=ty0+1=2t2+1,即E(2t2+1,2t),
故线段MN的中垂线方程为:y﹣2t=﹣t(x﹣2t2﹣1),
令y=0,则Q(2t2+3,0),
所以|FQ|=|22+3﹣1|=8,
解得t![]() ,
,
所以直线l的斜率k![]() ;
;
(2)点M恒在以FP为直径的圆外,则∠FMP为锐角,等价于![]() 0,
0,
设M(![]() ,y1),F(1,0),P(x0,0),
,y1),F(1,0),P(x0,0),
则![]() (x0
(x0![]() ,﹣y1),
,﹣y1),![]() (1
(1![]() ,﹣y1),
,﹣y1),
故![]() (x0
(x0![]() )(1
)(1![]() )+y12
)+y12![]() (1
(1![]() )x0>0恒成立,
)x0>0恒成立,
令t![]() ,t>0,原式等价于t2+3t+(1﹣t)x0>0对任意t>0恒成立,
,t>0,原式等价于t2+3t+(1﹣t)x0>0对任意t>0恒成立,
即t2+(3﹣x0)4+x0>0对任意t>0恒成立,
令h(t)=t2+(3﹣x0)4+x0,t>0,
①△=(3﹣x0)2﹣4x0<0,即1<x0<9,
② ,解得0≤x0≤1,又因为x0≠1,故x0∈[0,1),
,解得0≤x0≤1,又因为x0≠1,故x0∈[0,1),
综上所述x0∈[0,1)∪(1,9).


科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,点E是棱
,点E是棱![]() 的中点.
的中点.

(1)求证:![]() 平面ABC;
平面ABC;
(2)在棱CA上是否存在一点M,使得EM与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才能:礼乐射御书数,某校国学社团周末开展“六艺”课程讲座活动,每天连排六节,每艺一节,排课有如下要求:“礼”和“数”不能相邻,“射”和“乐”必须相邻,则“六艺”课程讲座不同的排课顺序共有( )
A.24种B.72种C.96种D.144种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,正确命题的个数有( )
①![]() ,
,![]()
②命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
③“若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于2”的逆命题是真命题
中至少有一个不小于2”的逆命题是真命题
④复数![]() ,则
,则![]() 的充分不必要条件是
的充分不必要条件是![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,AB=2,![]() ,D为AC上的一点(不含端点),将△BCD沿直线BD折起,使点C在平面ABD上的射影O在线段AB上,则线段OB的取值范围是( )
,D为AC上的一点(不含端点),将△BCD沿直线BD折起,使点C在平面ABD上的射影O在线段AB上,则线段OB的取值范围是( )
A.(![]() ,1)B.(
,1)B.(![]() ,
,![]() )C.(
)C.(![]() ,1)D.(0,
,1)D.(0,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() 是平面
是平面![]() 内的一组基向量,
内的一组基向量,![]() 为
为![]() 内的定点,对于
内的定点,对于![]() 内任意一点
内任意一点![]() ,当
,当![]() 时,则称有序实数对
时,则称有序实数对![]() 为点
为点![]() 的广义坐标,若点
的广义坐标,若点![]() 、
、![]() 的广义坐标分别为
的广义坐标分别为![]() 、
、![]() ,对于下列命题:
,对于下列命题:
① 线段![]() 、
、![]() 的中点的广义坐标为
的中点的广义坐标为![]() ;
;
② A、![]() 两点间的距离为
两点间的距离为![]() ;
;
③ 向量![]() 平行于向量
平行于向量![]() 的充要条件是
的充要条件是![]() ;
;
④ 向量![]() 垂直于向量
垂直于向量![]() 的充要条件是
的充要条件是![]() .
.
其中的真命题是________(请写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中医药,是包括汉族和少数民族医药在内的我国各民族医药的统称,是反映中华民族对生命、健康和疾病的认识,具有悠久历史传统和独特理论及技术方法的医药学体系,是中华民族的瑰宝.某科研机构研究发现,某品种中医药的药物成分甲的含量![]() (单位:克)与药物功效
(单位:克)与药物功效![]() (单位:药物单位)之间具有关系
(单位:药物单位)之间具有关系![]() .检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为
.检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为![]() 克,则估计这批中医药的药物功效的平均值为( )
克,则估计这批中医药的药物功效的平均值为( )
A.22药物单位B.20药物单位C.12药物单位D.10药物单位
查看答案和解析>>
科目:高中数学 来源: 题型:
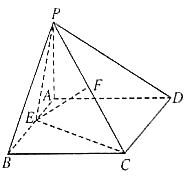
【题目】如图所示,四棱锥![]() 的底面是边长为2的正方形,平面
的底面是边长为2的正方形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 的中点,问边
的中点,问边![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ,并求此时点
,并求此时点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com