
【题目】中国古代儒家要求学生掌握六种基本才能:礼乐射御书数,某校国学社团周末开展“六艺”课程讲座活动,每天连排六节,每艺一节,排课有如下要求:“礼”和“数”不能相邻,“射”和“乐”必须相邻,则“六艺”课程讲座不同的排课顺序共有( )
A.24种B.72种C.96种D.144种
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线E的参数方程为![]() (
(![]() 为参数),以O为极点,x轴非负半轴为极轴建立极坐标系,直线
为参数),以O为极点,x轴非负半轴为极轴建立极坐标系,直线![]() ,
,![]() 的极坐标方程分别为
的极坐标方程分别为![]() ,
,![]() ,
,![]() 交曲线E于点A,B,
交曲线E于点A,B,![]() 交曲线E于点C,D.
交曲线E于点C,D.
(1)求曲线E的普通方程及极坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线的极坐标方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为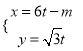 (
(![]() 为参数,
为参数, ![]() ).
).
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 上的动点
上的动点![]() 到直线
到直线![]() 的最大距离为
的最大距离为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 为抛物线
为抛物线![]() 过焦点
过焦点![]() 的弦,已知以
的弦,已知以![]() 为直径的圆与
为直径的圆与![]() 相切于点
相切于点![]() .
.
(1)求![]() 的值及圆的方程;
的值及圆的方程;
(2)设![]() 为
为![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的切线,切点为
的切线,切点为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直线l过抛物线C:y2=4x的焦点F,且与抛物线C交于M,N两点,且点M在x轴上方.
(1)若线段MN的垂直平分线交x轴于点Q,若|FQ|=8,求直线l的斜率;
(2)设点P(x0,0),若点M恒在以FP为直径的圆外,求x0的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .把
.把![]() 沿着
沿着![]() 翻折至
翻折至![]() 的位置,
的位置,![]() 平面
平面![]() ,连结
,连结![]() ,如图2.
,如图2.
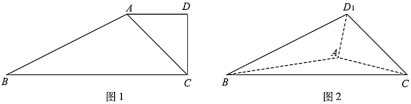
(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com