
【题目】如图,正四棱锥S-ABCD中,SA=AB=2,E,F,G分别为BC,SC,CD的中点.设P为线段FG上任意一点.
(1)求证:EP⊥AC;
(2)当P为线段FG的中点时,求直线BP与平面EFG所成角的余弦值.

【答案】(1)见解析;(2) ![]()
【解析】试题分析:(1)先证AC⊥平面SBD,再证平面EFG∥平面BSD,即得AC⊥平面GEF,因此可得EP⊥AC;(2)过B作BH⊥GE于H,根据三垂线定理可得∠BPH就是直线BP与平面EFG所成的角.再解三角形可得直线BP与平面EFG所成角的余弦值.
试题解析:(1)证明 设AC交BD于O点,
∵S-ABCD为正四棱锥,
∴SO⊥底面ABCD,BD⊥AC,
又AC平面ABCD,
∴SO⊥AC,∵BD∩SO=O,
BD平面SBD,SO平面SBD,
∴AC⊥平面SBD,
∵E,F,G分别为BC,SC,CD的中点,
∴FG∥SD,BD∥EG.
又FG∩EG=G,SD∩BD=D,
FG平面EFG,EG平面EFG,
SDBSD,BD平面BSD,
∴平面EFG∥平面BSD,
∴AC⊥平面GEF.
又∵PE平面GEF,∴PE⊥AC.
(2)解 过B作BH⊥GE于H,连接PH,
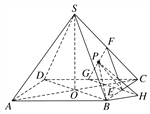
∵BD⊥AC,BD∥GH,
∴BH∥AC,
由(1)知AC⊥平面GEF,
则BH⊥平面GEF.
∴∠BPH就是直线BP与平面EFG所成的角.
在Rt△BHP中,BH=![]() ,PH=
,PH=![]() ,PB=
,PB=![]() ,
,
故cos∠BPH=![]() =
=![]() .
.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,且
,且![]() 与短轴的一个端点Q构成一个等腰直角三角形,点P(
与短轴的一个端点Q构成一个等腰直角三角形,点P(![]() )在椭圆
)在椭圆![]() 上,过点
上,过点![]() 作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆
作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆![]() 于A,B,C,D且M,N分别是弦AB,CD的中点
于A,B,C,D且M,N分别是弦AB,CD的中点
(1)求椭圆的方程
(2)求证:直线MN过定点R(![]() )
)
(3)求![]() 面积的最大值
面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 在点(1,1)处的切线方程为x+y=2.
在点(1,1)处的切线方程为x+y=2.
(1)求a,b的值;
(2)对函数f(x)定义域内的任一个实数x,不等式f(x)-![]() <0恒成立,求实数m的取值范围.
<0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
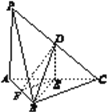
【题目】如图,在三棱锥P-ABC中,D,E,F分别为PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.
求证:(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
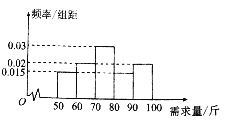
【题目】在某单位的食堂中,食堂每天以10元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂购进了80斤米粉,以![]() (斤)(其中
(斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (元)表示利润.
(元)表示利润.
(1)计算当天米粉需求量的平均数,并直接写出需求量的众数和中位数;
(2)估计该天食堂利润不少于760元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 的四个顶点在椭圆
的四个顶点在椭圆![]() :
: ![]() 上,对角线
上,对角线![]() 所在直线的斜率为
所在直线的斜率为![]() ,且
,且![]() ,
, ![]() .
.
(1)当点![]() 为椭圆
为椭圆![]() 的上顶点时,求
的上顶点时,求![]() 所在直线方程;
所在直线方程;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com