
在△ABC中,O为中线AM上的一个动点,若 ,则
,则 的最小值是
的最小值是
-2
【解析】
试题分析:
由题意画出草图分析,由于在△ABC中,O为中线AM上的一个动点,所以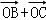 =2
=2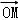 ,所以
,所以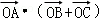 ═
═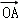 ?2
?2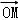 ,而|OA|+|OM|=2≥2
,而|OA|+|OM|=2≥2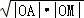 利用均值不等式即可求得解:由题意画出草图:
利用均值不等式即可求得解:由题意画出草图:
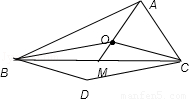
由于点M为△ABC中边BC的中点,∴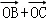 =2
=2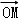 ,
,
∴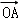 ?(
?(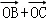 )=
)=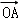 ?2
?2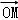 =﹣2|OA|?|OM|.
=﹣2|OA|?|OM|.
∵O为中线AM上的一个动点,即A、O、M三点共线
∴|AM|=|OA|+|OM|=2≥2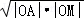 (当且仅当“OA=OM“时取等号)?|OA|?|OM|≤1,
(当且仅当“OA=OM“时取等号)?|OA|?|OM|≤1,
又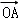 ?2
?2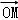 =﹣2|OA|?|OM|≥﹣2,所以则
=﹣2|OA|?|OM|≥﹣2,所以则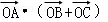 的最小值为﹣2.
的最小值为﹣2.
故答案为-2.
考点:三角形的中线
点评:该试题考查了三角形的中线以及向量的平行四边形法则的运用,属于基础题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| C | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com