
 如图,AB与圆O相切于点B,CD为圆O上两点,延长AD交圆O于点E,BF∥CD且交ED于点F
如图,AB与圆O相切于点B,CD为圆O上两点,延长AD交圆O于点E,BF∥CD且交ED于点F分析 (Ⅰ)根据BF∥CD便有∠EDC=∠BFD,再根据同一条弦所对的圆周角相等即可得出∠EBC=∠BFD,∠BCE=∠BDF,这样即可得出:△BCE与△FDB相似;
(Ⅱ)根据条件便可得出∠EBC=∠FBD,再由上面即可得出∠FBD=∠BFD,这样即可得出△FDB为等腰直角三角形,从而可求出BD=$\sqrt{2}$,根据射影定理即可求出AD•ED的值.
解答 解:
(Ⅰ)证明:∵BF∥CD;
∴∠EDC=∠BFD,
又∠EBC=∠EDC,
∴∠EBC=∠BFD,
又∠BCE=∠BDF,
∴△BCE∽△FDB.
(Ⅱ)因为∠EBF=∠CBD,所以∠EBC=∠FBD,
由(Ⅰ)得∠EBC=∠BFD,所以∠FBD=∠BFD,
又因为BE为圆O的直径,
所以△FDB为等腰直角三角形,BD=$\frac{\sqrt{2}}{2}$BF=$\sqrt{2}$,
因为AB与圆O相切于B,所以EB⊥AB,即AD•ED=BD2=2.
点评 考查内错角相等,同条弦所对的圆周角相等,以及三角形相似的判定定理,直径所对的圆周角为直角,以及射影定理.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2\sqrt{5}}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,7} | B. | {(3,7)} | C. | (3,7) | D. | [3,7] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
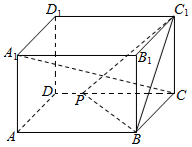 如图,长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1,点P是CD上的一点,PC=λPD.
如图,长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1,点P是CD上的一点,PC=λPD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com