
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
分析 此题是充分性,必要性的判定可先令a=-2看能不能得出函数f(x)=x2+ax+1只有一个零点,若能得出充分性成立否则不成立;然后看函数f(x)=x2+ax+1只有一个零点能不能得出a=-2,若能得出则必要性成立否则不成立.
解答 解:若a=-2,则函数f(x)=x2-2x+1,令f(x)=0,则(x-1)2=0,故x=1,
所以当a=-2函数f(x)=x2+ax+1只有一个零点1,
即“a=-2”是“函数f(x)=x2+ax+1只有一个零点”的充分条件;
若函数f(x)=x2+ax+1只有一个零点,即函数f(x)的图象与x轴只有一个交点,也即f(x)=0有且只有一个实根,所以△=a2-4=0,所以a=±2,
所以“a=-2”不是“函数f(x)=x2+ax+1只有一个零点”的必要条件.
故选:A.
点评 本题主要考查了必要条件,充分条件,充要条件的判定,属常考题型.解题的策略是先看前者能不能推出后者再看后者能不能推出后者然后再利用充分性、必要性的定义得出结论.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
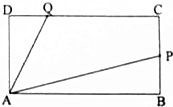 如图,矩形ABCD中,AB=4,AD=2,点P为BC的中点,且$\overrightarrow{DQ}$=λ$\overrightarrow{DC}$(λ∈R).
如图,矩形ABCD中,AB=4,AD=2,点P为BC的中点,且$\overrightarrow{DQ}$=λ$\overrightarrow{DC}$(λ∈R).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB与圆O相切于点B,CD为圆O上两点,延长AD交圆O于点E,BF∥CD且交ED于点F
如图,AB与圆O相切于点B,CD为圆O上两点,延长AD交圆O于点E,BF∥CD且交ED于点F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
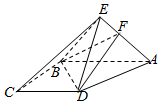 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB,点F满足$\overrightarrow{AF}$=2$\overrightarrow{FE}$.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB,点F满足$\overrightarrow{AF}$=2$\overrightarrow{FE}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
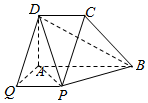 如图,在几何体ABCDQP中,AD⊥平面ABPQ,AB⊥AQ,AB∥CD∥PQ,CD=AD=AQ=PQ=$\frac{1}{2}$AB.
如图,在几何体ABCDQP中,AD⊥平面ABPQ,AB⊥AQ,AB∥CD∥PQ,CD=AD=AQ=PQ=$\frac{1}{2}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
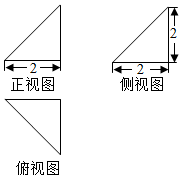
| A. | 2 | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $2\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com