
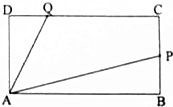
 如图,矩形ABCD中,AB=4,AD=2,点P为BC的中点,且$\overrightarrow{DQ}$=λ$\overrightarrow{DC}$(λ∈R).
如图,矩形ABCD中,AB=4,AD=2,点P为BC的中点,且$\overrightarrow{DQ}$=λ$\overrightarrow{DC}$(λ∈R).分析 (Ⅰ)根据平面向量的基本定理即可用$\overrightarrow{AB}$和$\overrightarrow{AD}$表示$\overrightarrow{AP}$;
(Ⅱ)若$\overrightarrow{AQ}$•$\overrightarrow{DC}$=4时,利用向量数量积的公式建立方程关系即可求λ的值.
解答 解:(Ⅰ)$\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{BP}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BC}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$.
(Ⅱ)在矩形ABCD中AD⊥DC,
则$\overrightarrow{AD}$•$\overrightarrow{DC}$=0,
∵$\overrightarrow{AQ}$•$\overrightarrow{DC}$=($\overrightarrow{AD}$+$\overrightarrow{DQ}$)•$\overrightarrow{DC}$=($\overrightarrow{AD}$+λ$\overrightarrow{DC}$)•$\overrightarrow{DC}$=$\overrightarrow{AD}$•$\overrightarrow{DC}$+λ•$\overrightarrow{DC}$2=16λ=4,
∴λ=$\frac{1}{4}$
点评 本题主要考查向量基本定理的应用以及向量数量积公式的应用,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | 5,15,25,35,45 | B. | 4,19,34,49,63 | C. | 7,23,39,55,71 | D. | 17,26,35,44,53 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在区间[0,$\frac{π}{2}$]上是减函数 | B. | 函数f(x)的图象关于原点对称 | ||
| C. | f(x)的最小正周期为$\frac{π}{2}$ | D. | f(x)的值域为[-$\sqrt{2}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2\sqrt{5}}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,7} | B. | {(3,7)} | C. | (3,7) | D. | [3,7] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
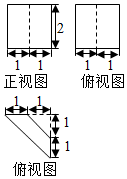 已知一个几何体的三视图如图所示,则该几何体的外接球的体积为( )
已知一个几何体的三视图如图所示,则该几何体的外接球的体积为( )| A. | 4$\sqrt{3}$π | B. | 2$\sqrt{3}π$ | C. | $\frac{7\sqrt{14}}{3}$π | D. | $\frac{14\sqrt{7}}{3}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com