Question

在四边形ABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，P为四边形ABCD外一点，PA⊥平面ABCD，E为PD的中点，PA＝2AB＝2．

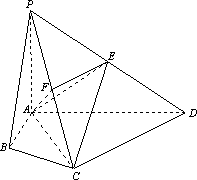
(1)若F为PC的中点，求证PC⊥平面AEF；

(2)求证CE∥平面PAB．

Answer 1

答案：
解析：

解：(1)∵PA＝CA，F为PC的中点， 　　∴AF⊥PC．　　2分 　　∵PA⊥平面ABCD，∴PA⊥CD．∵AC⊥CD，PA∩AC＝A， 　　∴CD⊥平面PAC．∴CD⊥PC． 　　∵E为PD中点，F为PC中点，∴EF∥CD．则EF⊥PC．　　5分 　　∵AF∩EF＝F，∴PC⊥平面AEF．　　6分 　　(2)证法一： 　　取AD中点M，连EM，CM．则EM∥PA． 　　∵EM平面PAB，PA平面PAB，∴EM∥平面PAB．　　8分 　　在Rt△ACD中，∠CAD＝60°，AC＝AM＝2，∴∠ACM＝60°．而∠BAC＝60°， 　　∴MC∥AB． 　　∵MC平面PAB，AB平面PAB，∴MC∥平面PAB．　　10分 　　∵EM∩MC＝M， 　　∴平面EMC∥平面PAB．∵EC平面EMC，∴EC∥平面PAB．　　12分 　　证法二： 　　延长DC、AB，设它们交于点N，连PN． 　　∵∠NAC＝∠DAC＝60°，AC⊥CD，∴C为ND的中点．　　8分 　　∵E为PD中点，∴EC∥PN．　　10分 　　∵EC平面PAB，PN平面PAB，∴EC∥平面PAB．　　12分