
分析 化简集合A、B,
(1)根据并集的定义求出A∪B;
(2)根据补集与交集的定义进行计算即可;
(3)化简集合C,根据A∩C≠∅求出a的取值范围.
解答 解:A={x|x2-2x-8≤0}={x|-2≤x≤4},…(2分)
B={x|$\frac{x-6}{x+1}$<0}={x|-1<x<6},…(4分)
(1)A∪B={x|-2≤x<6};…(6分)
(2)CUA={x|x<-2或x>4},…(8分)
(CUA)∩B={x|4<x<6};…(10分)
(3)C={x|x-a>0}={x|x>a},…(12分)
且A∩C≠∅,
所以a的取值范围是a<4.…(14分)
点评 本题考查了集合的化简与运算问题,是基础题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形,俯视图是圆心角为$\frac{π}{2}$的扇形,则该几何体的侧面积为( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形,俯视图是圆心角为$\frac{π}{2}$的扇形,则该几何体的侧面积为( )| A. | 2 | B. | 4+π | C. | 4+$\sqrt{2}$π | D. | 4+π+$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
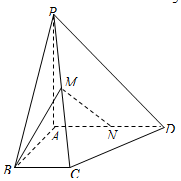 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
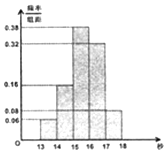 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com