
 ij��50��ѧ����һ�ΰ��ײ����У��ɼ�ȫ������13����18��֮�䣬�����Խ�������·�ʽ�ֳ����飺��һ��[13��14�����ڶ���[14��15��������������[17��18]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��
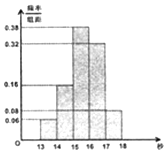
ij��50��ѧ����һ�ΰ��ײ����У��ɼ�ȫ������13����18��֮�䣬�����Խ�������·�ʽ�ֳ����飺��һ��[13��14�����ڶ���[14��15��������������[17��18]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ������ ��1����Ƶ�ʷֲ�ֱ��ͼ֪����������ײ��Գɼ���ƽ��ֵ��
��2����Ƶ�ʷֲ�ֱ��ͼ֪�ɼ���[13��14��������Ϊ3�ˣ���Ϊx��y��z���ɼ���[17��18��������Ϊ4�ˣ���ΪA��B��C��D�������оٷ�������¼���|m-n|��1���ĸ��ʣ�
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ֪�����ײ��Գɼ���ƽ��ֵΪ��
$\overline x=13.5��0.06+14.5��0.16+15.5��0.38+16.5��0.32+17.5��0.08$
=0.81+2.32+5.89+5.28+1.4=15.7����5�֣�
��2����Ƶ�ʷֲ�ֱ��ͼ֪��
�ɼ���[13��14��������Ϊ50��0.06=3�ˣ���Ϊx��y��z������6�֣�
�ɼ���[17��18��������Ϊ50��0.08=4�ˣ���ΪA��B��C��D����7�֣�
��m��n��[13��14��ʱ����xy��xz��yz��3�����������8�֣�
��m��n��[17��18��ʱ����AB��AC��AD��BC��BD��CD��6�����������9�֣�
��m��n�ֱ���[13��14����[17��18����ʱ��
| A | B | C | D | |
| x | xA | xB | xC | xD |
| y | yA | yB | yC | yD |
| z | zA | zB | zC | zD |
���� ���⿼��ƽ��ֵ����������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ���Ƶ�ʷֲ�ֱ��ͼ�����ʵĺ������ã�


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
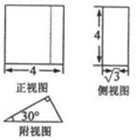
| A�� | $24+12\sqrt{3}$ | B�� | $24+5\sqrt{3}$ | C�� | $12+15\sqrt{3}$ | D�� | $12+12\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 90�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{16}$ | B�� | $\frac{1}{8}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ε�ֱ��ͼ������ƽ���ı��� | |
| B�� | ���ε�ֱ��ͼ������ƽ���ı��� | |
| C�� | ���ε�ֱ��ͼ���������� | |
| D�� | ���ഹֱ������ֱ�ߵ�ֱ��ͼһ���ǻ��ഹֱ������ֱ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com