
分析 根据题意:g(x)=lnx(x≥1),图象过(1,0),所以二次函数图象过(1,0),即k=1,可得函数f(x)=x2-x,当0<x<1时,要使f(x)对一切正实数x恒成立,即x2-x≥-x3+(a+1)x2-ax.利用二次函数的性质求解即可.
解答 解:由题意:函数f(x)=kx2-kx,g(x)=$\left\{\begin{array}{l}lnx,x≥1\\-{x^3}+({a+1}){x^2}-ax,0<x<1\end{array}$,
当g(x)=lnx(x≥1),图象过(1,0),使得不等式f(x)≥g(x)对一切正实数x恒成立的实数k存在且唯一,即kx2-kx-lnx≥0,令m(x)=kx2-kx-lnx≥0
则m′(x)=2kx-k-$\frac{1}{x}$≥0.
实数k存在且唯一,当x=1时,解得k=1.
即k=1.可得函数f(x)=x2-x.
当0<x<1时,要使f(x)≥g(x)对一切正实数x恒成立,即x2-x≥-x3+(a+1)x2-ax.
令h(x)=x2-ax+a-1≥0,
∵对一切正实数x恒成立且唯一,
∴△=a2-4(a-1)=0,
解得:a=2.
故答案为:2.
点评 本题考查了分段函数的值域来求解恒成立问题.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
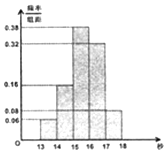 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | C. | 奇函数或偶函数 | D. | 非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,3) | D. | (3,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com