
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 由题意由于图中已有了两两垂直的三条直线,所以可以建立空间直角坐标系,先准确写出个点的坐标,利用线面角和线与平面的法向量所构成的两向量的夹角之间的关系即可求解.
解答 解:如图所示,以O为原点建立空间直角坐标系O-xyz.
设OD=SO=OA=OB=OC=a,
则A(a,0,0),B(0,a,0),C(-a,0,0),P(0,-$\frac{a}{2}$,$\frac{a}{2}$).
则$\overrightarrow{CA}$=(2a,0,0),$\overrightarrow{PA}$=(-a,-$\frac{a}{2}$,$\frac{a}{2}$),
设平面PAC的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{2ax=0}\\{-ax-\frac{a}{2}y+\frac{a}{2}z=0}\end{array}\right.$,
可求得$\overrightarrow{n}$=(0,1,1),
则cos<$\overrightarrow{BC}$,$\overrightarrow{n}$>=$\frac{1}{2}$.
∴<$\overrightarrow{BC}$,$\overrightarrow{n}$>=60°,
∴直线BC与平面PAC所成的角为90°-60°=30°.
故选A.
点评 此题重点考查了直线与平面所成的角的概念及利用空间向量的方法求解空间中的直线与平面的夹角.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
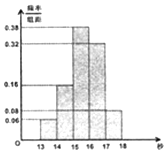 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | C. | 奇函数或偶函数 | D. | 非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1,-1 | B. | -1 | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com