
(本小题满分13分)经市场调查,某商场的一种商品在过去的一个月内(以30天计)销售价格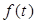 (元)与时间
(元)与时间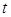 (天)的函数关系近似满足
(天)的函数关系近似满足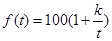 (
(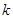 为正的常数),日销售量
为正的常数),日销售量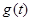 (件)与时间
(件)与时间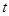 (天)的函数关系近似满足
(天)的函数关系近似满足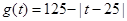 ,且第25天的销售金额为13000元.
,且第25天的销售金额为13000元.
(1)求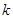 的值;
的值;
(2)试写出该商品的日销售金额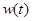 关于时间
关于时间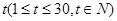 的函数关系式,并求前半个月销售金额
的函数关系式,并求前半个月销售金额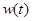 的最小值。
的最小值。
科目:高中数学 来源: 题型:解答题
(本小题满分16分)
有甲、乙两种商品,经销这两种商品所获的利润依次为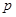 (万元)和
(万元)和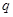 (万元),它们与投入的资金
(万元),它们与投入的资金 (万元)的关系,据经验估计为:
(万元)的关系,据经验估计为: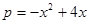 ,
, 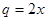 今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?
今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知函数 =
=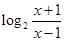 .
.
(1)判断函数 的奇偶性,并证明;
的奇偶性,并证明;
(2)求 的反函数
的反函数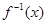 ,并求使得函数
,并求使得函数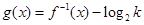 有零点的实数
有零点的实数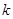 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数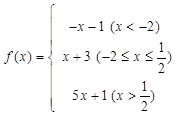 (
(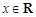 ),
),
(Ⅰ)求函数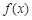 的最小值;
的最小值;
(Ⅱ)已知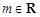 ,
,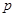 :关于
:关于 的不等式
的不等式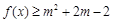 对任意
对任意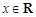 恒成立;
恒成立;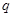 :函数
:函数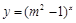 是增函数.若“
是增函数.若“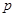 或
或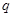 ”为真,“
”为真,“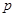 且
且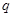 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)
如图,在半径为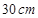 的
的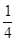 圆形(
圆形( 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料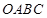 ,其中点
,其中点 在圆上,点
在圆上,点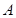 、
、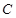 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮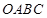 卷成一个以
卷成一个以 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长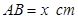 ,圆柱的体积为
,圆柱的体积为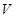
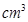 .
.
(1)写出体积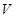 关于
关于 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)当 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积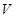 最大?最大体积是多少?
最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已
知投资生产这两种产品的有关数据如下表:(单位:万美元)
| 项目类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| A产品 | 10 | m | 5 | 100 |
| B产品 | 20 | 4 | 9 | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com