
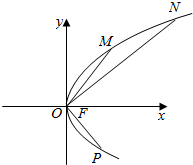
 已知F是抛物线C:y2=2px(p>0)的焦点,O为坐标原点.
已知F是抛物线C:y2=2px(p>0)的焦点,O为坐标原点.分析 (1)设M(x1,y1),N(x2,y2),直线MN的方程为y=kx+m,将直线方程与y2=2px联立,消去x,由韦达定理知y1+y2,y1y2.通过θ1+θ2=$\frac{π}{3}$时,利用直线的斜率以及两角和的正切函数,推出m,k的关系,得到直线MN恒过定点;
(2)假设存在点P,使得$\frac{OP}{FP}$达到最大值.设P($\frac{{m}^{2}}{2p}$,m),由抛物线的定义,再令t=$\frac{{m}^{2}}{2p}$+$\frac{p}{2}$,t>$\frac{p}{2}$,可得m2=2p(t-$\frac{p}{2}$)=2pt-p2,再由配方和二次函数的最值的求法,即可得到最大值,即可判断.
解答 (1)证明:设M(x1,y1),N(x2,y2),y2=2px,
由题意得x1≠x2且x1,x2≠0,
所以直线AB的斜率存在,设其方程为y=kx+m,
则x1=$\frac{{{y}_{1}}^{2}}{2p}$,x2=$\frac{{{y}_{2}}^{2}}{2p}$,
将y=kx+m与y2=2px联立消去x,得:ky2-2py+2pm=0.
则:y1+y2=$\frac{2p}{k}$,y1y2=$\frac{2pm}{k}$,
OM,ON的倾斜角分别为θ1、θ2,且θ1+θ2=$\frac{π}{3}$,
又tanθ1=$\frac{{y}_{1}}{{x}_{1}}$=$\frac{2p}{{y}_{1}}$,tanθ2=$\frac{{y}_{2}}{{x}_{2}}$=$\frac{2p}{{y}_{2}}$,
所以,$\sqrt{3}$=tan(θ1+θ2)=$\frac{tan{θ}_{1}+tan{θ}_{2}}{1-tan{θ}_{1}tan{θ}_{2}}$
=$\frac{\frac{2p}{{y}_{1}}+\frac{2p}{{y}_{2}}}{1-\frac{4{p}^{2}}{{y}_{1}{y}_{2}}}$=$\frac{2p({y}_{1}+{y}_{2})}{{y}_{1}{y}_{2}-4{p}^{2}}$=$\frac{2p•\frac{2p}{k}}{\frac{2pm}{k}-4{p}^{2}}$=$\frac{2p}{m-2pk}$.
即m=2pk-$\frac{2p}{\sqrt{3}}$,
直线MN的方程为y=kx+2pk-$\frac{2p}{\sqrt{3}}$,即y+$\frac{2p}{\sqrt{3}}$=k(x+2p),
所以直线MN恒过定点(-2p,-$\frac{2\sqrt{3}}{3}$p);
(2)假设存在点P,使得$\frac{OP}{FP}$达到最大值.
设P($\frac{{m}^{2}}{2p}$,m),由抛物线的定义可得|PF|=$\frac{{m}^{2}}{2p}$+$\frac{p}{2}$,
$\frac{|OP|}{|PF|}$=$\frac{\sqrt{{m}^{2}+\frac{{m}^{4}}{4{p}^{2}}}}{\frac{{m}^{2}}{2p}+\frac{p}{2}}$,
令t=$\frac{{m}^{2}}{2p}$+$\frac{p}{2}$,t>$\frac{p}{2}$,可得m2=2p(t-$\frac{p}{2}$)=2pt-p2,
即有$\frac{|OP|}{|PF|}$=$\sqrt{\frac{{t}^{2}+pt-\frac{3}{4}{p}^{2}}{{t}^{2}}}$=$\sqrt{-\frac{3}{4}•\frac{{p}^{2}}{{t}^{2}}+\frac{p}{t}+1}$
=$\sqrt{-\frac{3}{4}(\frac{p}{t}-\frac{2}{3})^{2}+\frac{4}{3}}$,当$\frac{p}{t}$=$\frac{2}{3}$即t=$\frac{3}{2}$p>$\frac{1}{2}$p,即有m=±$\sqrt{2}$p,
取得最大值$\frac{2\sqrt{3}}{3}$.
故存在点P(p,±$\sqrt{2}$p),使得$\frac{OP}{FP}$达到最大值.
点评 本题考查抛物线的定义、方程和性质,考查直线恒过定点的证明,并求出该定点的坐标,解题时要认真审题,注意函数与方程思想的合理运用,换元法的运用,考查运算能力,属于中档题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)过点P(-2$\sqrt{3}$,1),且离心率e=$\frac{\sqrt{3}}{2}$,过右焦点F的直线l交椭圆于M,N两点.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)过点P(-2$\sqrt{3}$,1),且离心率e=$\frac{\sqrt{3}}{2}$,过右焦点F的直线l交椭圆于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com