
【题目】已知函数![]() ,
, ![]() .
.
(I)求![]() 的单调区间;
的单调区间;
(II)若对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:对函数求导,针对参数![]() 进行讨论,研究函数得单调性;第二步为恒成立问题,当
进行讨论,研究函数得单调性;第二步为恒成立问题,当![]() 时,由于
时,由于![]() 不满足题意要求,当
不满足题意要求,当![]() 时,求出函数
时,求出函数![]() 的最大值,要使
的最大值,要使![]() 在
在![]() 上恒成立,只需
上恒成立,只需![]() ,从而求出
,从而求出![]() 的范围.
的范围.
试题解析:(I)![]() , 当
, 当![]() 时,
时, ![]() 恒成立,则
恒成立,则![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,令
时,令![]() ,则
,则![]() .则
.则![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(II)方法1:
当![]() 时,因为
时,因为![]() ,
,
所以不会有![]() ,
, ![]() .
.
②当![]() 时,由(I)知,
时,由(I)知, ![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
所以![]() ,
, ![]() 等价于
等价于![]() .即
.即![]() .
.
设![]() ,由(I)知
,由(I)知![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以
,所以![]() 的解为
的解为![]() .
.
故![]() ,
, ![]() 时,实数
时,实数![]() 的取值范围是
的取值范围是![]() .
.
方法2: ![]() ,
, ![]() 等价于
等价于![]() .令
.令![]() ,则
,则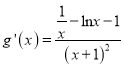 .
.
令![]() ,则
,则![]() .
.
因为当![]() ,
, ![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,可得
,可得![]() 和
和![]() 在
在![]() 上的情况如下:
上的情况如下:
|
|
|
|
| + | 0 | - |
| 单调递增 | 单调递减 |
所以![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
因此![]() ,
, ![]() 等价于
等价于![]() .
.
故![]() ,
, ![]() 时,实数
时,实数![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】据市场分析,南雄市精细化工园某公司生产一种化工产品,当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数;当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元,为二次函数的顶点.写出月总成本y(万元)关于月产量x(吨)的函数关系.已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届广西陆川县中学高三文上学期二模】已知函数![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(III)在(II)的条件下,对任意的![]() ,求证:
,求证: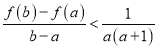 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(
,(![]() ).
).
(1)若函数![]() 与
与![]() 的图象在
的图象在![]() 上有两个不同的交点,求实数
上有两个不同的交点,求实数![]() 的取值范围;
的取值范围;
(2)若在![]() 上不等式
上不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:对于![]() 时,任意
时,任意![]() ,不等式
,不等式![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届安徽百校论坛高三文上学期联考二】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,第(1)问 6 分,第(2)问 6 分)
某品牌新款夏装即将上市,为了对夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
连锁店 | A店 | B店 | C店 | |||
售价 | 80 | 86 | 82 | 88 | 84 | 90 |
销售量 | 88 | 78 | 85 | 75 | 82 | 66 |
(1)以三家连锁店分别的平均售价和平均销量为散点,求出售价与销量的回归直线方程![]() ;
;
(2)在大量投入市场后,销售量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该款夏装在销售上获得最大利润,该款夏装的单价应定为多少元(保留整数)?
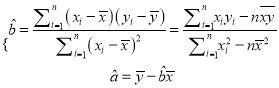
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
在平面直角坐标系中,有三个点的坐标分别是![]() .
.
(1)证明:A,B,C三点不共线;
(2)求过A,B的中点且与直线![]() 平行的直线方程;
平行的直线方程;
(3)设过C且与AB所在的直线垂直的直线为![]() ,求
,求![]() 与两坐标轴围成的三角形的面积.
与两坐标轴围成的三角形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com