
【题目】某中学的高二(1)班男同学有![]() 名,女同学有
名,女同学有![]() 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个![]() 人的课外兴趣小组.
人的课外兴趣小组.
(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出![]() 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】试题分析:本题主要考查分层抽样、随机事件的概率等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,在抽样过程中每个个体被抽到的机会均等,都等于![]() ,从而得到某同学被抽到的概率,利用分层抽样求出男女生人数;第二问,把抽取的3名男同学和1名女同学记为
,从而得到某同学被抽到的概率,利用分层抽样求出男女生人数;第二问,把抽取的3名男同学和1名女同学记为![]() ,分别写出任取2人的所有情况,在其中找出有1名女同学的情况,再求概率.
,分别写出任取2人的所有情况,在其中找出有1名女同学的情况,再求概率.
试题解析:(1)![]()
![]() 某同学被抽到的概率为
某同学被抽到的概率为![]() 2分
2分
设有![]() 名男同学,则
名男同学,则![]() ,
,![]()
![]() 男、女同学的人数分别为
男、女同学的人数分别为![]() 4分
4分
(2)把![]() 名男同学和
名男同学和![]() 名女同学记为
名女同学记为![]() ,则选取两名同学的基本事件
,则选取两名同学的基本事件![]()
![]() 共
共![]() 种,其中有一名女同学的有
种,其中有一名女同学的有![]() 种 (8分)
种 (8分)
![]() 选出的两名同学中恰有一名女同学的概率为
选出的两名同学中恰有一名女同学的概率为![]() 10分
10分


科目:高中数学 来源: 题型:
【题目】x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.
(1)请写出程序框图所表示的函数表达式;
(2)求输出的y(y<5)的概率;
(3)求输出的y(6<y≤8)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m,n均大于0,则 ![]() 的最小值为( )
的最小值为( )
A.2
B.4
C.8
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
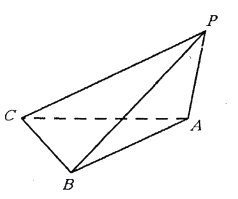
【题目】已知三棱锥 ![]() ,底面
,底面 ![]() 是以
是以 ![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, ![]() ,
, ![]() ,二面角
,二面角 ![]() 的大小为
的大小为 ![]() .
.
(1)求直线 ![]() 与平面
与平面 ![]() 所成角的大小;
所成角的大小;
(2)求二面角 ![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB= ![]() ,AF=1,G为线段AD上的任意一点.
,AF=1,G为线段AD上的任意一点. 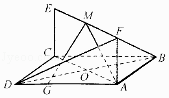
(1)若M是线段EF的中点,证明:平面AMG⊥平面BDF;
(2)若N为线段EF上任意一点,设直线AN与平面ABF,平面BDF所成角分别是α,β,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
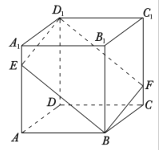
【题目】如图,在正方体![]() 中,过对角线
中,过对角线![]() 的一个平面交
的一个平面交![]() 于点
于点![]() ,交
,交![]() 于
于![]() .
.
①四边形![]() 一定是平行四边形;
一定是平行四边形;
②四边形![]() 有可能是正方形;
有可能是正方形;
③四边形![]() 在底面
在底面![]() 内的投影一定是正方形;
内的投影一定是正方形;
④四边形![]() 有可能垂直于平面
有可能垂直于平面![]() .
.
以上结论正确的为_______________.(写出所有正确结论的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com