
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,![]() ,记
,记![]() 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
【答案】(1)942;(2)50万元
【解析】试题分析:(1)根据题意,首先确定X的所有可能取值,然后利用统计表格,借助古典概型的公式计算对应的概率,进而利用期望公式求解;(2)利用独立重复实验的概率计算公式求解满足条件的概率,明确![]() 为该销售商购进并销售一辆二手车的利润的可能性,得到分布列和利润期望值.
为该销售商购进并销售一辆二手车的利润的可能性,得到分布列和利润期望值.
(Ⅰ)由题意可知X的可能取值为![]() ,
,
由统计数据可知:
![]() ,
,
![]() .
.
所以![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
所以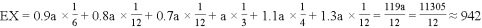 .
.
(Ⅱ) ①由统计数据可知任意一辆该品牌车龄已满三年的二手车为事故车的概率为![]() ,三辆车中至多有一辆事故车的概率为
,三辆车中至多有一辆事故车的概率为![]() .
.
![]() 为该销售商购进并销售一辆二手车的利润,
为该销售商购进并销售一辆二手车的利润,![]() 的可能取值为
的可能取值为![]() .
.
所以![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
所以![]() .
.
所以该销售商一次购进100辆该品牌车龄已满三年的二手车获得利润的期望值为![]() 万元.
万元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分,第(1)问 6 分,第(2)问 6 分)
某品牌新款夏装即将上市,为了对夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
连锁店 | A店 | B店 | C店 | |||
售价 | 80 | 86 | 82 | 88 | 84 | 90 |
销售量 | 88 | 78 | 85 | 75 | 82 | 66 |
(1)以三家连锁店分别的平均售价和平均销量为散点,求出售价与销量的回归直线方程![]() ;
;
(2)在大量投入市场后,销售量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该款夏装在销售上获得最大利润,该款夏装的单价应定为多少元(保留整数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
在平面直角坐标系中,有三个点的坐标分别是![]() .
.
(1)证明:A,B,C三点不共线;
(2)求过A,B的中点且与直线![]() 平行的直线方程;
平行的直线方程;
(3)设过C且与AB所在的直线垂直的直线为![]() ,求
,求![]() 与两坐标轴围成的三角形的面积.
与两坐标轴围成的三角形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
观看方式 年龄(岁) | 电视 | 网络 |
| 150 | 250 |
| 120 | 80 |

![]()
求:(I)假设同一组中的每个数据用该组区间的中点值代替,求非常喜欢《人民的名义》这部电视剧的观众的平均年龄;
(II)根据表1,通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为集合A,B={x|x<a}.
的定义域为集合A,B={x|x<a}.
(1)求集合A;
(2)若AB,求a的取值范围;
(3)若全集U={x|x≤4},a=-1,求U A及A∩(U B).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() ,
,![]() ,(
,(![]() 为自然对数的底数).是否存在常数
为自然对数的底数).是否存在常数![]() ,使
,使![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com