Question

3．（1）在等腰直角三角形ABC中，在斜边AB上任取一点M，求AM＜AC的概率．
（2）在等腰直角三角形ABC中，过直角顶点C在∠ACB内部任作一条射线CM，与线段交于点M，求AM＜AC的概率．
（3）在等腰直角三角形ABC内任取点P，连接CP的射线交斜边AB与M，求AM＜AC的概率．

Answer 1

分析 （1）欲求AM＜AC的概率，先求出M点可能在的位置的长度，AC的长度，再让两者相除即可．
（2）由于过直角顶点C在∠ACB内部任作一射线CM，故可以认为所有可能结果的区域为∠ACB，可将事件A构成的区域为∠ACC'，以角度为“测度”来计算．
（3）与（2）相同．

解答 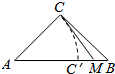解：（1）在等腰直角三角形ABC中，设AC长为1，则AB长为$\sqrt{2}$，
在AC′上取点D，使AC′=1，则若M点在线段AB上，满足条件．
∵AC′=1，AB=$\sqrt{2}$
∴AM＜AC的概率为$\frac{AC′}{AB}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$
（2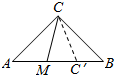）在AB上取AC'=AC，则$∠ACC'=\frac{{{{180}°}-45°}}{2}={67.5°}$．
记A={在∠ACB内部任作一射线CM，与线段AB交于点M，AM＜AC}，
则所有可能结果的区域为∠ACB，
事件A构成的区域为∠ACC'．
又∠ACB=90°，∠ACC'=67.5°．
∴$P（A）=\frac{{{{67.5}°}}}{{{{90}°}}}=\frac{3}{4}$．
（3）在AB上取AC'=AC，则$∠ACC'=\frac{{{{180}°}-45°}}{2}={67.5°}$．
记A={在∠ACB内部任作一射线CM，与线段AB交于点M，AM＜AC}，
则所有可能结果的区域为∠ACB，
事件A构成的区域为∠ACC'．
又∠ACB=90°，∠ACC'=67.5°．
∴$P（A）=\frac{{{{67.5}°}}}{{{{90}°}}}=\frac{3}{4}$．

点评 本题考查几何概型．在利用几何概型的概率公式来求其概率时，几何“测度”可以是长度、面积、体积、角度等，其中对于几何度量为长度，面积、体积时的等可能性主要体现在点落在区域Ω上任置都是等可能的．