
给出命题:若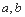 是正常数,且
是正常数,且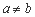 ,
,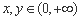 ,则
,则 (当且仅当
(当且仅当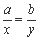 时等号成立). 根据上面命题,可以得到函数
时等号成立). 根据上面命题,可以得到函数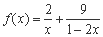 (
(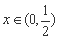 )的最小值及取最小值时的x值分别为( )
)的最小值及取最小值时的x值分别为( )
A.11+6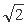 ,
,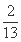 B.11+6
B.11+6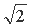 ,
, C.25,
C.25,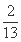
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )
A. 假设三内角都不大于60度
B. 假设三内角都大于60度
C. 假设三内角至多有一个大于60度
D. 假设三内角至多有两个大于60度
查看答案和解析>>
科目:高中数学 来源: 题型:
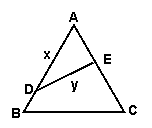
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪, 图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1).设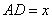 (x≥0),
(x≥0),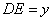 ,求用
,求用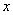 表示
表示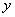 的函数关系
的函数关系
式,并求函数的定义域;
(2).如果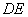 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短,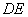 的
的
位置应在哪里?如果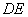 是参观线路,则希望它最长,
是参观线路,则希望它最长,
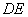 的位置又应在哪里?请予证明.
的位置又应在哪里?请予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
)设函数
(1)写出函数f (x)的最小正周期及单调递增区间;
(2)当 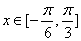 时,函数f (x)的最小值为2,求此时函数f (x)的最大值,并指出x取何值时函数f (x)取得最大值.
时,函数f (x)的最小值为2,求此时函数f (x)的最大值,并指出x取何值时函数f (x)取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
在三棱锥S—ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2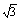 ,M、N分别为AB、SB的中点, 求点B到平面CMN的距离.
,M、N分别为AB、SB的中点, 求点B到平面CMN的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com