
【题目】在平面直角坐标系中,顶点为原点的抛物线![]() ,它是焦点为椭圆
,它是焦点为椭圆![]() 的右焦点.
的右焦点.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过抛物线![]() 的焦点作互相垂直的两条直线分别交抛物线
的焦点作互相垂直的两条直线分别交抛物线![]() 于
于![]() 四点,求四边形
四点,求四边形![]() 的面积的最小值.
的面积的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为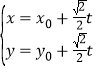 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 的直角坐标为
的直角坐标为![]() ,求直线
,求直线![]() 及曲线
及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在圆
在圆![]() 上,直线
上,直线![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数,
为参数,![]() 为直线倾斜角).以平面直角坐标系的原点为极点,
为直线倾斜角).以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)当![]() 时,直线
时,直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,当
两点,当![]() 面积最大时,求直线
面积最大时,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,右顶点为A,上顶点为B,若
,右顶点为A,上顶点为B,若![]() ,
,![]() ,
,![]() 成等比数列,椭圆C上的点到焦点
成等比数列,椭圆C上的点到焦点![]() 的距离的最大值为
的距离的最大值为![]() .
.
![]() 求椭圆C的标准方程;
求椭圆C的标准方程;
![]() 过该椭圆的右焦点
过该椭圆的右焦点![]() 作倾角为
作倾角为![]() 的直线与椭圆交于M,N两点,求
的直线与椭圆交于M,N两点,求![]() 的内切圆的半径.
的内切圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的方程为:
的方程为:![]()
![]() 当极点
当极点![]() 到直线
到直线![]() 的距离为
的距离为![]() 时,求直线
时,求直线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若直线
若直线![]() 与曲线
与曲线![]() 有两个不同的交点,求实数
有两个不同的交点,求实数![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节期间,某超市准备举办一次有奖促销活动,若顾客一次消费达到400元则可参加一次抽奖活动,超市设计了两种抽奖方案.
方案一:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得60元的返金券,若抽到白球则获得20元的返金券,且顾客有放回地抽取3次.
方案二:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得80元的返金券,若抽到白球则未中奖,且顾客有放回地抽取3次.
(1)现有两位顾客均获得抽奖机会,且都按方案一抽奖,试求这两位顾客均获得180元返金券的概率;
(2)若某顾客获得抽奖机会.
①试分别计算他选择两种抽奖方案最终获得返金券的数学期望;
②为了吸引顾客消费,让顾客获得更多金额的返金券,该超市应选择哪一种抽奖方案进行促销活动?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com