
分析 (1)直接利用作差法,再进行因式分解,分析证明即可.
(2)直接利用作差法,结合平方、开方,然后分析证明即可.
解答 证明:(1)3a3+2b3-(3a2b+2ab2)=3a3-3a2b+2b3-2ab2=3a2(a-b)+2b2(b-a)=(3a2-2b2)(a-b).
因为a≥b>0,
所以a-b≥0,3a2-2b2≥0,
从而(3a2-2b2)(a-b)≥0,
即3a3+2b3≥3a2b+2ab2.
(2)∵|1-ab|2-|a-b|2=1+a2b2-a2-b2=(a2-1)(b2-1).
∵|a|<1,|b|<1,
∴a2-1<0,b2-1<0.
∴|1-ab|2-|a-b|2>0,
故有|1-ab|>|a-b|.
点评 本题考查不等式的证明,作差法的应用,考查学生分析解决问题的能力,属于中档题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:填空题
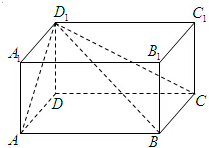 长方体ABCD-A1B1C1D1中,AA1=1,D1C与平面ABCD所成的角为30°,BC1与BC所成的角为45°,则二面角D1-AC-B的正切值为$-\frac{2\sqrt{3}}{3}$.
长方体ABCD-A1B1C1D1中,AA1=1,D1C与平面ABCD所成的角为30°,BC1与BC所成的角为45°,则二面角D1-AC-B的正切值为$-\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| P(K2>k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
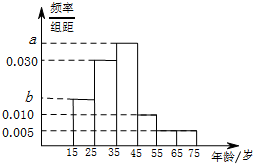 2016年全国两会,即中华人民共和国第十二届全国人民代表大会第四次会议和中国人民政治协商会议第十二届全国委员会第四次会议,分别于2016年3月5日和3月3日在北京开幕.为了解哪些人更关注两会,某机构随抽取了年龄在15~75岁之间的100人进行调查,并按年龄绘制的频率分布直方图如图所示,其分组区间为:[15,25),[25,35),[35,45),[55,65),[65,75].把年龄落在区间[15,35)和[35,75]内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”和“中老年人”的人数之比为9:11.
2016年全国两会,即中华人民共和国第十二届全国人民代表大会第四次会议和中国人民政治协商会议第十二届全国委员会第四次会议,分别于2016年3月5日和3月3日在北京开幕.为了解哪些人更关注两会,某机构随抽取了年龄在15~75岁之间的100人进行调查,并按年龄绘制的频率分布直方图如图所示,其分组区间为:[15,25),[25,35),[35,45),[55,65),[65,75].把年龄落在区间[15,35)和[35,75]内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”和“中老年人”的人数之比为9:11.| 关注 | 不关注 | 合计 | |
| 青少年人 | 15 | ||
| 中老年人 | |||
| 合计 | 50 | 50 | 100 |
| P(K2≥k0) | 0.05 | 0.01 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com