
研究函数的对称中心有如下结论:如果存在实数a, b使![]() 恒成立,则(a, b)为函数
恒成立,则(a, b)为函数![]() 的图像的对称中心.
的图像的对称中心.
(1)求证函数![]() 的图像的对称中心为(0,1),并求函数
的图像的对称中心为(0,1),并求函数![]() 的图象的对称中心;
的图象的对称中心;
(2)试用函数的性质及图象变换解释:“如果存在实数a, b使![]() 恒成立,则(a, b)为函数
恒成立,则(a, b)为函数![]() 的图象的对称中心.”
的图象的对称中心.”
(3)是否存在函数![]() ,使函数
,使函数![]() 的图象有相同的对称中心(c,d)?请对
的图象有相同的对称中心(c,d)?请对![]() 时,说明你的结论与理由.
时,说明你的结论与理由.
解:(1)对于函数![]() 恒成立,
恒成立,
所以![]() 的图象的对称中心为(0,1).
的图象的对称中心为(0,1).
设![]()
![]() 的对称中心为(a,b)
的对称中心为(a,b)
则![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
所以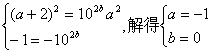
所以![]() 的图象的对称中心为(-1,0)
的图象的对称中心为(-1,0)
(2)由![]()
令![]() 为奇函数,
为奇函数,
其图像关于原点(0,0)对称,
而函数![]() 的图象可由
的图象可由![]() 向右平移a(a>0)或向左平移
向右平移a(a>0)或向左平移![]() 单位或不进行左右平移(a=0),向上平移b(b>0)或向下平移-b(b<0)或不进行上下平移(b=0)单位得到,所以
单位或不进行左右平移(a=0),向上平移b(b>0)或向下平移-b(b<0)或不进行上下平移(b=0)单位得到,所以![]() 的图像的对称中心为(a,b).
的图像的对称中心为(a,b).
说明:(1)中分别说明![]() ,仿(2)也可!
,仿(2)也可!
(3)假设存在函数![]() ,使
,使![]() 有相同的对称中心(c,d)且
有相同的对称中心(c,d)且![]() ,则
,则![]() ,且
,且
![]()
所以![]() 的两个实数,
的两个实数,
而该方程![]() 当
当![]() 时,
时,![]() ,
,
所以假设错误.
所以,不存在函数![]() 有相同的对称中心(c,d),
有相同的对称中心(c,d),
其中![]() .
.


科目:高中数学 来源: 题型:
| 1 |
| 2012 |
| 2 |
| 2012 |
| 4022 |
| 2012 |
| 4023 |
| 2012 |
查看答案和解析>>
科目:高中数学 来源:河北省衡水中学2011-2012学年高二下学期期中考试数学文科试题 题型:022
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:![]() (x)是函数f(x)的导函数,
(x)是函数f(x)的导函数,![]() (x)是
(x)是![]() (x)的导函数,若方程
(x)的导函数,若方程![]() (x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心.若
(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心.若![]() ,请你根据这一发现,求:
,请你根据这一发现,求:
(1)函数![]() 的对称中心为________.
的对称中心为________.
(2)![]() =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北衡水中学高三上学期期中考试文科数学试卷(解析版) 题型:填空题
对于三次函数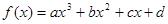
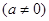 ,给出定义:
,给出定义: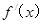 是函数
是函数 的导函数,
的导函数,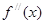 是
是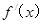 的导函数,若方程
的导函数,若方程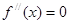 有实数解
有实数解 ,则称点
,则称点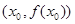 为函数
为函数 的“拐点”。某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心。若
的“拐点”。某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心。若 ,请你根据这一发现,求:(1)函数
,请你根据这一发现,求:(1)函数 的对称中心为__________;(2)
的对称中心为__________;(2) =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省汕头市高三五月高考前模拟理科数学试卷(解析版) 题型:选择题
设函数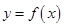 的定义域为
的定义域为 ,若对于任意
,若对于任意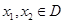 且
且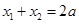 ,恒有
,恒有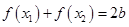 ,则称点
,则称点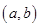 为函数
为函数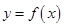 图象的对称中心.研究并利用函数
图象的对称中心.研究并利用函数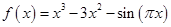 的对称中心,可得
的对称中心,可得
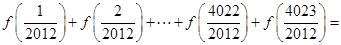
A.4023 B.-4023 C.8046 D.-8046
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com