
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
| 11 |
| 3 |
| x-1 |
| x+1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2014届广东省广州市高三9月三校联考理科数学试卷(解析版) 题型:选择题
函数 的定义域为D,若对于任意
的定义域为D,若对于任意
 ,当
,当 时,都有
时,都有 ,则称函
,则称函
数 在D上为非减函数,设函数
在D上为非减函数,设函数 在[0,1]上为非减函数,且满足以下三个条件:
在[0,1]上为非减函数,且满足以下三个条件:
① ; ②
; ② ; ③
; ③ .
.
则 等于( )
等于( )
A. B.
B. C.
C. D.无法确定
D.无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
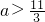 ;
;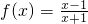 ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 11 |
| 3 |
| x-1 |
| x+1 |
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com