B
分析:由数列为等差数列,利用等差数列的性质得到a
3+a
5=2a
4,a
8+a
14=a
6+a
16=2a
11,化简已知的等式,可得出a
4+a
11的值,再根据等差数列的性质得到a
1+a
14=a
4+a
11,由a
4+a
11的值得到a
1+a
14的值,然后利用等差数列的前n项和公式表示出该数列的前14项之和,将a
1+a
14的值代入即可求出值.
解答:∵数列{a
n}为等差数列,
∴a
3+a
5=2a
4,a
8+a
14=a
6+a
16=2a
11,
又4(a
3+a
4+a
5)+3(a
6+a
8+a
14+a
16)=36,
∴12a
4+12a
11=36,即a
4+a
11=3,
∵a
1+a
14=a
4+a
11=3,
则该数列的前14项和S
14=
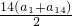
=21.
故选B
点评:此题考查了等差数列的性质,以及等差数列的求和公式,熟练掌握性质及公式是解本题的关键.

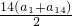 =21.
=21.
