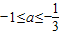给定曲线f(x)=ax3+x2(a≠0).
(1)若a=1,过点P(1,2)引曲线的切线,求切线方程;
(2)若过曲线上的点Q引曲线的切线只有一条,求点Q的坐标;
(3)若x∈(0,1)时,以曲线段上任一点为切点的切线斜率的绝对值不大于1,求实数a的取值范围.
【答案】
分析:(1)先求函数的导函数,然后讨论点P是否为切点,当P(1,2)为切点时,切线斜率k=f'(1),然后利用点斜式方程可求出切线方程,当P(1,2)不是切点时,设切点为T(x
,x
3+x
2),切线斜率k=f'(x
),然后根据k=k
PT建立等式关系,求出切点,从而求出切线方程;
(2)设Q(x
1,ax
13+x
12),以Q为切点时必然存在一条切线,求出切线方程,然后与曲线联立方程组,使关于x的方程只有一个根x
1,△=0,可求出点Q的坐标;
(3)由题意得:-1≤3ax
2+2x≤1,x∈(0,1)恒成立,然后将a分离出来得
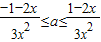
,然后分别研究左边函数在x∈(0,1)的最大值,右边函数在x∈(0,1)的最小值,即可求出a的取值范围.
解答:解:(1)f(x)=x
3+x
2,f'(x)=3x
2+2x
①当P(1,2)为切点时,切线斜率k=f'(1)=5,此时切线方程为y-2=5(x-1),即y=5x-3.
②当P(1,2)不是切点时,设切点为T(x
,x
3+x
2),切线斜率k=f'(x
)=3x
3+2x
另一方面,k=k
PT=
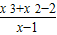
∴
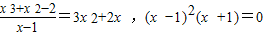
∵x
≠1,∴x
=-1,∴T(-1,0),此时切线y=x+1
综上,所求的切线为y=5x-3或y=x+1.
(2)设Q(x
1,ax
13+x
12),以Q为切点时必然存在一条切线.
切线斜率k=f'(x
1)=3ax
12+2x
1,
切线方程为:y-(ax
13+x
12)=3(ax
12+2x
1)(x-x
1),联立曲线y=ax
3+x
2,
得(x-x
1)[ax
2+(ax
1+1)x-2ax
12-x
1]=0,
由于这样的切线只有一条,所以上述关于x的方程只有一个根x
1,
即二次方程ax
2+(ax
1+1)x-2ax
12-x
1=0只有一个根x
1,
显然把x=x
1代入满足,故△=(ax
1+1)
2+4a(2ax
12+x
1)=0
化简为:△=9a
2x
12+6ax
1+1=(3ax
1+1)
2=0,解得x
1=-
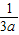
,得

(3)由题意得:-1≤3ax
2+2x≤1,x∈(0,1)恒成立
∴
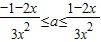
∵
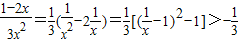
,
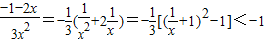
,
∴
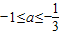 点评:
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及恒成立问题,同时考查了分类讨论的数学思想,属于中档题.

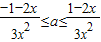 ,然后分别研究左边函数在x∈(0,1)的最大值,右边函数在x∈(0,1)的最小值,即可求出a的取值范围.
,然后分别研究左边函数在x∈(0,1)的最大值,右边函数在x∈(0,1)的最小值,即可求出a的取值范围.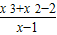
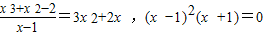
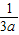 ,得
,得
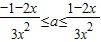
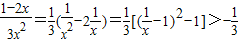 ,
,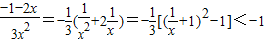 ,
,