
解答:解法一:由直线l:3x+y-6=0和圆x2+y2-2y-4=0的方程得
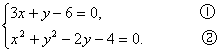
消去y,得x2-3x+2=0.
因为Δ=(-3)2-4×1×2=1>0,所以直线l与圆相交,有两个公共点.
由x2-3x+2=0,得x1=2,x2=1.
把x1=2代入方程①,得y1=0;把x2=1代入方程①,得y2=3.
所以直线l与圆相交有两个公共点,它们的坐标分别是(2,0)和(1,3).
解法二:圆x2+y2-2y-4=0的方程可化为x2+(y-1)2=5,其圆心C的坐标为(0,1),半径长为5,圆心C到直线l的距离d=![]() =
=![]() <
<![]() .
.
所以直线l与圆相交,有两个公共点.(以后同解法一)
点评:比较两种解法,我们可以看出,几何法判断要比代数法判断快得多,但是若要求交点,仍须联立方程组求解.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、y=3x+2 | B、y=-3x+2 | C、x=3y+2 | D、x=-3y+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)P到点A(4,1)和B(0,4)的距离之差最大;
(2)Q到点A(4,1)和C(3,4)的距离之和最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com