
����Ŀ���ס��ҡ��������ĸ�����ͬʱ��ijһ�������ͬһ�������˶�����·��![]()
![]() ����ʱ��
����ʱ��![]() �ĺ�����ϵʽ�ֱ�Ϊ
�ĺ�����ϵʽ�ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() �������½��ۣ�
�������½��ۣ�
�ٵ�![]() ʱ����������ǰ�棻
ʱ����������ǰ�棻
�ڵ�![]() ʱ����������ǰ�棻
ʱ����������ǰ�棻
�۵�![]() ʱ����������ǰ�棬��
ʱ����������ǰ�棬��![]() ʱ������������棻
ʱ������������棻
�ܱ�������������ǰ�棬Ҳ��������������棻
���������һֱ�˶���ȥ������������ǰ����Ǽף�
���У���ȷ���۵����Ϊ ������ȷ���۵���Ŷ����ϣ��������������÷֣���
���𰸡��ۢܢ�
��������·��![]() ����ʱ��
����ʱ��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
������Ӧ�ĺ���ģ�ͷֱ���ָ���ͺ��������κ�����һ�κ������Ͷ����ͺ���ģ�ͣ�
��![]() ʱ��
ʱ��![]() ,������ٲ���ȷ��
,������ٲ���ȷ��
��![]() ʱ��
ʱ��![]() ��������ڲ���ȷ��
��������ڲ���ȷ��
�����ͺ����ı仯���ȿ��������![]() ʱ���ס��ҡ��������ĸ������غϣ��Ӷ���֪��
ʱ���ס��ҡ��������ĸ������غϣ��Ӷ���֪��![]() ʱ����������ǰ�棬��
ʱ����������ǰ�棬��![]() ʱ������������棬�������ȷ��
ʱ������������棬�������ȷ��
ָ���������仯��������죬���˶���ʱ���㹻��ʱ����ǰ�������һ���ǰ���ָ���ͺ����˶������壬��һ���Ǽ����壬���������ȷ��
��϶����ͺ�ָ���ͺ�����ͼ��仯�������֪��������������ǰ�棬Ҳ��������������棬�������ȷ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a����1������f��x��=|x3��1|+x3+ax��x��R����
��������f��x������Сֵ��
������֪����ʵ��m��n��m��n��1����������t0�ʣ�m��n�����ܴ���������ͬ��t1 �� t2�ʣ�1��+�ޣ���
ʹ��f��t0����2=f��t1��=f��t2������֤�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f�䣨x�����溯��f��x����x��R���ĵ�������f����1��=0����x��0ʱ��xf�䣨x����f��x����0����ʹ��f��x����0������x��ȡֵ��Χ�ǣ� ��
A.�����ޣ���1���ȣ�0��1��
B.����1��0���ȣ�1��+�ޣ�
C.�����ޣ���1���ȣ���1��0��
D.��0��1���ȣ�1��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������P��ABCD�У������DZ߳�Ϊa�������Σ�����PD��a��PA��PC��![]() a��
a��
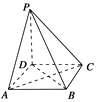
(1)��֤��PD��ƽ��ABCD��
(2)��֤��ƽ��PAC��ƽ��PBD��
(3)������P��AC��D������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ֱ������ϵ��ԭ���غϣ�������x����������غϣ�ԲC�ļ������Ǧ�=2asin�ȣ�ֱ��l�IJ��������� 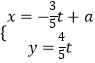 ��tΪ��������
��t��������
��1����a=2��MΪֱ��l��x��Ľ��㣬N��ԲC��һ���㣬��|MN|�����ֵ��
��2����ֱ��l��ԲC�صõ��ҳ�Ϊ ![]() ����a��ֵ��
����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������p������y=sin2x����С������Ϊ ![]() ������q������y=cosx��ͼ�����ֱ��x=
������q������y=cosx��ͼ�����ֱ��x= ![]() �Գƣ��������ж���ȷ���ǣ� ��
�Գƣ��������ж���ȷ���ǣ� ��
A.p��
B.�Vq��
C.p��q��
D.p��q��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����
����![]() .
.
��1������![]() ��ֵ��
��ֵ��
��2���ö���֤������![]() ��
��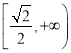 �ϵ���������
�ϵ���������
��3�������![]() �ķ���
�ķ���![]() ������Ϊ
������Ϊ![]() �������Ƿ����ʵ��
�������Ƿ����ʵ��![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() �������
�������![]() ��
��![]() ������������ڣ����
������������ڣ����![]() ��ȡֵ��Χ����������˵������.
��ȡֵ��Χ����������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ex��ax2��bx��1������a��b��R��e=2.718 28��Ϊ��Ȼ�����ĵ�����
��1����g��x���Ǻ���f��x���ĵ�����������g��x��������[0��1]�ϵ���Сֵ��
��2����f��1��=0������f��x�������䣨0��1��������㣬֤����e��2��a��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ��ͨ���������������۶��Ԥ���֪����ҵ��Ʒ�Ĺ���x����λ������Ԫ�������۶�y����λ������Ԫ��֮�������¶�Ӧ���ݣ�
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
�ɱ��е����ݵ����Իع鷽��Ϊ ![]() =
= ![]() x+
x+ ![]() ������
������ ![]() =6.5���ɴ�Ԥ�����Ϊ7����Ԫʱ�����۶�Ϊ��Ԫ��
=6.5���ɴ�Ԥ�����Ϊ7����Ԫʱ�����۶�Ϊ��Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com