
| A. | 一班:总体均值为2,总体方差为2 | B. | 二班:总体均值为3,中位数为3 | ||
| C. | 三班:总体均值为2,总体方差大于0 | D. | 四班:中位数为2,众数为2 |
分析 根据均值,中位数、众数、方差的意义,结合特殊数值逐一判断.
解答 解:A.总体均值为2,总体方差为2,当总体平均数是2,若有一个数据n超过5,则方差就会大于$\frac{1}{5}$[(n-2)2]≥$\frac{16}{5}$>2,由此每天迟到都不超过5人次,
B.总体均值为3,说明数据集中于3,中位数为3说明迟到3人的天数较多,但不能说明每天迟到都不超过5人,比如1,3,3,3,5
C.总体均值为2,说明数据集中于2,总体方差大于0,仍有可能某天迟到学生超过5人次
D 中位数为2,众数为2,比如0,1,2,2,6,6>5,不合要求.
故选:A.
点评 本题考查数据的几个特征量,这几个量各自表示数据的一个方面,有时候一个或两个量不能说明这组数据的特点,若要掌握这组数据则要全面掌握.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 4 | C. | 0或4 | D. | 1或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 15 | C. | 16 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
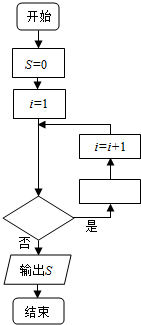 如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.
如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x∈Z|x≥3} | C. | {3,4} | D. | {1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com